Hypothesis testing > Degrees of freedom
Degrees of freedom of an estimate is the number of independent pieces of information that went into calculating the estimate. Determination of the degrees of freedom is based on the statistical procedure you’re using, but for most common analyses it is usually calculated by subtracting one from the number of items in the sample.
Let’s say you were finding the mean weight loss for a low-carb diet. You could use four people, giving three degrees of freedom (4 – 1 = 3), or you could use 100 people with df = 99.
As a formula, where “n” is the number of items in your sample:
Degrees of Freedom = n – 1
Watch the video for an overview:
Can’t see the video? Click here to watch it on YouTube.
Contents:
- Why do we subtract 1 from the number of items?
- Degrees of freedom: Two Samples
- Degrees of Freedom in ANOVA
- Why Do Critical Values Decrease While DF Increase?
- History of Degrees of Freedom
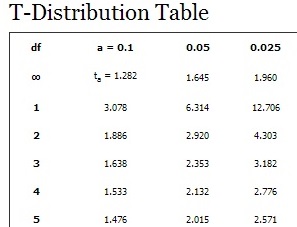
Why do we subtract 1 from the number of items?
Another way to look at degrees of freedom is that they are the number of values that are free to vary in a data set. What does “free to vary” mean? Here’s an example using the mean (average); If the data set must add up to a specific mean, the numbers chosen are constrained by other values chosen.
Let’s say you pick a set of numbers that have a mean of 10. You might pick: (9, 10, 11) or (8, 10, 12) or (5, 10, 15).
Once you have chosen the first two numbers in the set, the third is fixed. In other words, you can’t choose the third item in the set. The only numbers that are free to vary are the first two. You can pick 9 + 10, but once you’ve made that decision you must choose 11 to give you the mean of 10. So degrees of freedom for a set of three numbers is TWO.
If you wanted to find a confidence interval for a sample, degrees of freedom is n – 1. “N’ can also be the number of classes or categories. See: Critical chi-square value for an example.
Back to Top
Degrees of Freedom: Two Samples
If you have two samples and want to find a parameter, like the mean, you have two “n”s to consider (sample 1 and sample 2). Degrees of freedom in that case is:
Degrees of Freedom (Two Samples): (N1 + N2) – 2.
In a two sample t-test, use the formula
df = N – 2
because there are two parameters to estimate.
Degrees of Freedom in ANOVA
Degrees of freedom becomes a little more complicated in ANOVA tests. Instead of a simple parameter (like finding a mean), ANOVA tests involve comparing known means in sets of data. For example, in a one-way ANOVA you are comparing two means in two cells. The grand mean (the average of the averages) would be:
Mean 1 + mean 2 = grand mean.
What if you chose mean 1 and you knew the grand mean? You wouldn’t have a choice about Mean2, so your degrees of freedom for a two-group ANOVA is 1.
Two Group ANOVA df1 = n – 1
For a three-group ANOVA, you can vary two means so degrees of freedom is 2.
It’s actually a little more complicated because there are two degrees of freedom in ANOVA: df1 and df2. The explanation above is for df1. Df2 in ANOVA is the total number of observations in all cells – degrees of freedoms lost because the cell means are set.
Two Group ANOVA df2 = n – k
The “k” in that formula is the number of cell means or groups/conditions.
For example, let’s say you had 200 observations and four cell means. Degrees of freedom in this case would be: Df2 = 200 – 4 = 196.
Back to Top
Why Do Critical Values Decrease While DF Increase?
Let’s take a look at the t-score formula in a hypothesis test:
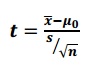
When n increases, the t-score goes up. This is because of the square root in the denominator: as it gets larger, the fraction s/√n gets smaller and the t-score (the result of another fraction) gets bigger. As the degrees of freedom are defined above as n-1, you would think that the t-critical value should get bigger too, but they don’t: they get smaller. This seems counter-intuitive.
However, think about what a t-test is actually for. You’re using the t-test because you don’t know the standard deviation of your population and therefore you don’t know the shape of your graph. It could have short, fat tails. It could have long skinny tails. You just have no idea. The degrees of freedom affect the shape of the graph in the t-distribution; as the df get larger, the area in the tails of the distribution get smaller. As df approaches infinity, the t-distribution will look like a normal distribution. When this happens, you can be certain of your standard deviation (which is 1 on a normal distribution).
Let’s say you took repeated sample weights from four people, drawn from a population with an unknown standard deviation. You measure their weights, calculate the mean difference between the sample pairs and repeat the process over and over. The tiny sample size of 4 will result a t-distribution with fat tails. The fat tails tell you that you’re more likely to have extreme values in your sample. You test your hypothesis at an alpha level of 5%, which cuts off the last 5% of your distribution. The graph below shows the t-distribution with a 5% cut off. This gives a critical value of 2.6. (Note: I’m using a hypothetical t-distribution here as an example–the CV is not exact).
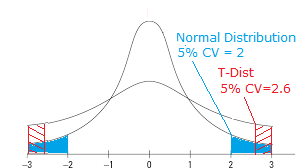
Now look at the normal distribution. We have less chance of extreme values with the normal distribution. Our 5% alpha level cuts off at a CV of 2.
Back to the original question “Why Do Critical Values Decrease While DF Increases?” Here’s the short answer:
Degrees of freedom are related to sample size (n-1). If the df increases, it also stands that the sample size is increasing; the graph of the t-distribution will have skinnier tails, pushing the critical value towards the mean.
History of Degrees of Freedom
English statistician Ronald Fisher popularized the idea of degrees of freedom. He is credited with explicitly defining the degrees-of-freedom concept, beginning with his 1915 paper on the distribution of the correlation coefficient [1]. His discovery of degrees of freedom was due in part by an error made by Karl Pearson, claimed that no correction in degrees of freedom are needed when parameters are estimated under the null hypothesis [2]. Fisher did not mince words when it came to Pearson’s error: In a volume of his collected works, Fisher wrote about Pearson, “If peevish intolerance of free opinion in others is a sign of senility, it is one which he had developed at an early age” [3].
Although Fisher is credited with the development of degrees of freedom in 1915, Carl Friedrich Gauss introduced the basic concept as early as 1821 [4]. However, its modern definition is thanks to English statistician William Sealy Gosset in his 1908 Biometrika article “The Probable Error of a Mean“, published under the pen name “Student.”
While Gosset [Student]did not use the term ‘degrees of freedom,’ he did explain the concept while developing Student’s t-distribution. Gosset and Fisher were in correspondence together and Fisher proved a geometrical formulation that Gosset had been working on [5].
Another way to look at Degrees of Freedom
If you still can’t wrap your head around the concept, don’t beat yourself up. Even the great Karl Pearson couldn’t hone in on its meaning without making an error! Many authors throughout the years have pointed out the esoteric nature of the term, including Walker [6], who said in 1940 that “For the person who is unfamiliar with N-dimensional geometry or who knows the contributions to modern sampling theory only from secondhand sources such as textbooks, this concept often seems almost mystical, with no practical meaning.”
According to Joseph Lee Rogers of Vanderbilt university [1], a simpler way to look at degrees of freedom is that it defines an accounting process that counts the flow of data from the statistical bank — into which we deposit data points — into the model. When you run a statistical analysis involving parameters (e.g., a t test or regression analysis), you withdraw money from the bank to pay for estimating the parameters in your model. Degrees of freedom is a count of the statistical money you have withdrawn from the bank and the statistical money still left in the bank.
References
[1] Rodgers JL. Degrees of Freedom at the Start of the Second 100 Years: A Pedagogical Treatise. Advances in Methods and Practices in Psychological Science. 2019;2(4):396-405. doi:10.1177/2515245919882050
[2] Stigler, S. Karl Pearson’s Theoretical Errors and the Advances They Inspired. Statistical Science, 2008, Vol. 23 No. 2, 261-271.
[3] Agresti, A. Historical Highlights in the Development of Categorical Data Analysis.
[4] Walker H. M. (1940). Degrees of freedom. Journal of Educational Psychology, 31, 253–269.
[6] Fisher R. A. (1915). Frequency distribution of the values of the correlation coefficient in samples from an indefinitely large population. Biometrika, 10, 507–521.