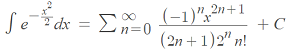Contents:
What is the 68 95 99.7 rule?
Watch the video for an overview:
When you use a standard normal distribution (aka Gaussian Distribution):
- About 68% of values fall within one standard deviation of the mean.
- About 95% of the values fall within two standard deviations from the mean.
- Almost all of the values—about 99.7%—fall within three standard deviations from the mean.
These facts are the 68 95 99.7 rule. It is sometimes called the Empirical Rule because the rule originally came from observations (empirical means “based on observation”).
The Normal/Gaussian distribution is the most common type of data distribution. All of the measurements are computed as distances from the mean and are reported in standard deviations.
The Gaussian curve is a symmetric distribution, so the middle 68.2% can be divided in two. Zero to 1 standard deviations from the mean has 34.1% of the data. The opposite side is the same (0 to -1 standard deviations). Together, this area adds up to about 68% of the data.
When to use the Rule
You can use the rule when you are told your data is normal, nearly normal, or if you have a unimodal distribution (i.e. one with a single peak) that is symmetric. If a question mentions a normal or nearly normal distribution, and you’re given standard deviations, that almost certainly means you can use the rule to approximate how many of your scores will fall within a certain number of standard deviations.
Example Question
The weights of stray dogs at a particular pound average 70 lbs with a standard deviation of 2.5 lbs. Assuming the weights follow a Gaussian distribution:
- What weight is 2 standard deviations below the mean?
- What weight is 1 standard deviation above the mean?
- The middle 68% of dogs weigh how much?
Answers:
- 2 standard deviations is 2 * 2.5 (5 lbs). So if a dog is 2 standard deviations below the mean they weigh 70 lbs – 5 lbs = 65 lbs.
- 1 standard deviation is 2.5 lbs, so a dog 1 standard deviation above the mean would weigh 70 lbs + 2.5 lbs = 72.5 lbs.
- The 68 95 99.7 Rule tells us that 68% of the weights should be within 1 standard deviation either side of the mean. 1 standard deviation above (given in the answer to question 2) is 72.5 lbs; 1 standard deviation below is 70 lbs – 2.5 lbs is 67.5 lbs. Therefore, 68% of dogs weigh between 67.5 and 72.5 lbs.
History of the 68 95 99.7 Rule
he 68 95 99.7 rule was first coined by Abraham de Moivre in 1733, 75 years before the normal distribution model was published. De Moivre worked in the developing field of probability. Perhaps his biggest contribution to statistics was the 1756 edition of The Doctrine of Chances, containing his work on the approximation to the binomial distribution by the normal distribution in the case of a large number of trials.
De Moivre discovered the 68 95 99.7 rule with an experiment. You can do your own experiment by flipping 100 fair coins. Note:
- How many heads you would expect to see; these are “successes” in this binomial experiment.
- The standard deviation.
- The upper and lower limits for the number of heads you would get 68% of the time, 95% of the time and 99.7% of the time
Empirical Rule & The Area Under the Curve
The 68-95-99.7 rule tells us the area under the curve for a normal distribution. In other words, it’s telling us values of the integral:
![]()
Where:
- fZ(z) is the normal distribution’s pdf

The integral can be evaluated for standard deviations to derive the empirical rule:

The exponential function e-z2/2 doesn’t have a simple antiderivative, so the integral has to be calculated with numerical integration. For example, as a Taylor series or with Riemann sums (Simpson’s rule is one of the better variants).
Taylor Series Steps
One way to define the exponential function e(x) is as a Taylor series for x = 0:
![]()
Using a little algebra, we can extend the definition to e-x2/2:
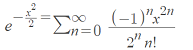
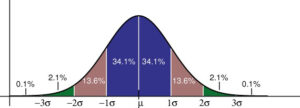
- Integrating:


- For the standard normal distribution cdf Φ, we want Φ(0) = ½:
 for x ≈ 0.
for x ≈ 0.
At 68%, the approximation for the empirical rule comes fairly close:
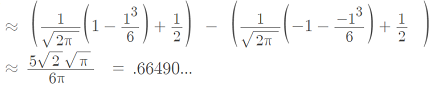
Empirical Research Definition
The word “empirical” means based on observation or experience rather than theory. While the empirical rule is a practical “rule of thumb”, empirical research is where you conduct “hands on” experimentation. In other words, you get your results from actual experience rather than from a theory or belief.
This type of research has four major characteristics:
- A research question is posed.
- The target behavior, population, or phenomena is defined.
- The process is described in detail so that the research can be verified and duplicated. For example, a researcher might include information about any use of instruments and control groups.
Calculus forms a foundation for many quantitative research methods and is an integral part of professional empirical research.
Examples of Empirical Research:
1. Pavlov’s Dog Experiments
Pavlov, most famous for his “Salivating Dogs,” actually won more acclaim for his empirical research involving the digestive system. Until Pavlov’s experiments, little was known about the digestive system. His carefully carried out and documented experiments on dogs resulted in him receiving the Nobel prize in physiology of Medicine in 1904.
2. Discovery of the DNA Double Helix
Watson and Crick discovered the double helix in 19531. Until their discovery, nothing was known about the structure of the smallest unit of genetic information known at the time–the gene. After many failed model-building attempts, they finally built a model that matched the known information about the gene’s structure. The actual proof of Watson and Crick’s work came much later when laboratory experiments by several researchers (including Arthur Kornberg, Matthew Meselson, Franklin Stahl and others) confirmed their findings.
The Empirical Research Cycle

This representation of DeGroot’s empirical cycle starts with observation. We notice something, and have a question about that “something” or want to change it. That leads to induction —forming a hypothesis statement. Next is deduction, where testable consequences of the hypothesis are formulated. The actual empirical (experimental) portion of the cycle comes next, followed by evaluation of the experimental results, which leads to more questions and the beginning of the cycle.
Writing the Empirical Research paper
The IMRaD Format
Many papers (usually scientific ones) that feature empirical research have a layout called “IMRaD,” which stands for:
- Introduction: background information such as similar studies, reasons for conducting the research and any additional information necessary to understand the paper’s contents.
- Methods: details about how the experiment was conducted.
- Results: presents the results along with any statistics or analysis performed on the results.
- and
- Discussion: discusses the implications of the results.
This is the same as the APA format’ the American Psychological Association uses IMRaD headings (see the Purdue OWL website for more information on formatting in APA style).
Papers that are written for empirical research should also (no brainer here) have a title. They should also have an abstract after the title, which is a summary of the paper’s contents.
Empirical Rule & Research: References
Blanco, M. & Ginovart, M. How to introduce historically the normal distribution in engineering education: a classroom experiment. Retrieved December 28 2015. http://upcommons.upc.edu/bitstream/handle/2117/6483/howtointroduce.pdf
Davis, Meselson and Stahl: The art of DNA replication. Available here.
Gonick, L. (2015). Cartoon Guide to Statistics. HarperCollins Publishers.
Kjos-Hanssen, B. (2019). Statistics for Calculus Students. Retrieved May 1, 2021 from: https://dspace.lib.hawaii.edu/bitstream/10790/4572/s4cs.pdf
Pyrczak, F. (2016). Writing Empirical Research Reports: A Basic Guide for Students of the Social and Behavioral Sciences. Routledge.