The amplitude of a function is a measure of the range’s variability: how the function varies between the midline (for example, the x-axis) and the maximum. In other words, the amplitude is half the distance between the maximum and minimum height, or how much the function goes up and down from the horizontal axis.
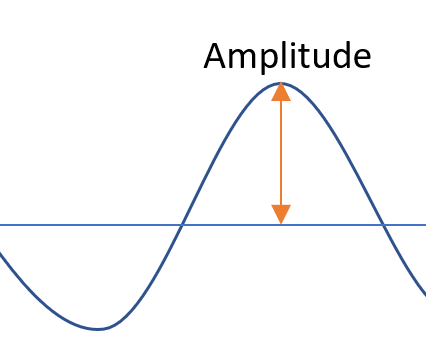
Amplitude of Functions: Trig Functions
Sine functions f(x) = a sin(x) and cosine functions f(x) = a cos(x) have positive amplitudes of |a|. Amplitudes are always positive, because they are distances [1].
The parent functions f(x) = sin(x) and f(x) = cos(x) have an amplitude of 1, reaching heights of a maximum of 1 above the x-axis and below the x-axis. In other words, if you change a, then the amplitude changes:
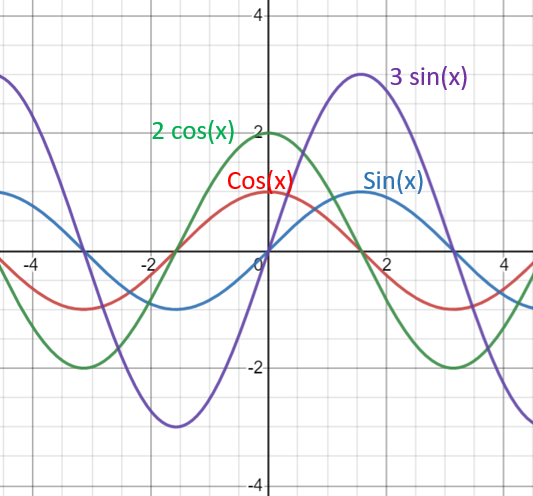
Several trig functions have ranges that go from negative to positive infinity, so they do not have amplitude [2]. These include:
- Cosecant function csc(x),
- Cotangent function cot(x),
- Secant function sec(x),
- Tangent function tan(x).
How to Find the Amplitude of a Function
- On a graph: Count the number of units from the x-axis to the max height of the function.
- With a formula: Look for the value of “a”. For example, y = 2 sin(x) has an amplitude of 2: if there’s no “a”, then the amplitude is 1. For example, y = sin(2x) has an amplitude of 1.
It isn’t always quite that easy. The following example shows a “trick” to watch out for on exams: extra numbers at the end of formulae.
Example question: What is the amplitude of a function defined as:
f(x) = −10 sin(π(x − ½)-1 ?
Solution:
- Find the absolute value of a, given here as -10. The absolute value of -10 is 10.
- Subtract 1 (because there’s a -1 at the end of the formula).
References
Amplitude cos/sin image graphed with Desmos.com.
[1] Thurston, D. Sine Transformations. Retrieved April 2, 2021 from: http://jwilson.coe.uga.edu/EMAT6680Fa2013/Thurston/Write-Ups/Write-up%201/SineTransformations.html
[2] Section 5.5: Trig Functions Translations and Dilations