L’Hospital’s rule (also spelled L’Hôpital’s) is a way to find limits using derivatives when you have indeterminate limits (e.g. {0/0} or {∞/∞}). In those cases, the “usual” ways of finding limits just don’t work. The rule also works for all limits at infinity, or one-sided limits.
L’Hospital’s rule doesn’t work in all cases. For example, it can’t be applied when you have a function of several variables, such as:
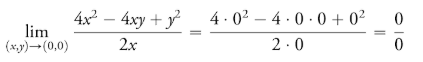
That said, if you’re learning about the rule in an early calculus class, it’s unlikely you’ll come across one of these curve balls: you’re much more likely to be given “simple” functions where the rule applies.
Formal Definition
The formal definition of L’Hospital’s rule looks a little ugly:

However, all it’s really saying is that in special cases you can use the limit of the derivative to find the limit of the function. More specifically, the limit of a quotient of functions (e.g. – ∞/∞) equals the quotient of their derivatives. That’s if the right-side limit is zero or infinity.
L’Hospital’s Rule: Example Problem 1
Find ![]()
Step 1: Take the limit of the function to make sure you have an indeterminate form.
The function is asking you to find the limit at x = 1, so:
- lim ln(x) = ln(1) = 0
- lim (x – 1 ) = 0
The limit on both sides is 0, so it is indeterminate.
Step 2: Identify f(x) and g(x) from your function (the two parts in the formal definition of the rule). The top function in the rule is f(x) and the bottom function is g(x). In this case,
- f(x) = ln(x)
- g(x) = (x – 1)
Step 3: Find the derivative for f(x) and g(x):
- D ln(x) = 1/x
- D (x – 1) = 1
Step 3: Form the new quotient then find the limit:
![]()
L’Hospital’s Rule: Example Problem 2
Use L’Hospital’s rule to find the limit as x approaches zero for the function sin(x)⁄x :
Step 1: Take the limit of the function to make sure you have an indeterminate form.
lim x→0 sin(x)⁄x = 0⁄0
If you don’t have an indeterminate form of the limit (i.e. if the numerator and the denominator in the fraction aren’t both zero or infinity), you don’t need L’Hospital’s rule.
Step 2: Identify f(x) and g(x) from your function. The top function is f(x) and the bottom function is g(x). In this case, f(x) is sin(x) and g(x) is x.
Step 3: Find the derivative for f(x) and g(x):
f'(sin x) = cos x
f'(x) = 1
Step 4: Take the limit of the derivative functions from Step 3:
lim x->0 (cos x) = 1
lim x->0 (x) = 1
Therefore, the limit of the function cos(x)⁄x = 1/1.
L’Hospital’s rule states that the limit of this derivative function is also the limit of the function itself, so:
lim →0 sin(x)⁄x = 1
That’s it!
References
Adillon, R. et al. (2015). Mathematics for Economics and Business. Edicions Universitat Barcelona.
Stewart, J. Calculus.