Estimators > Shrinkage Estimator
What is Shrinkage?
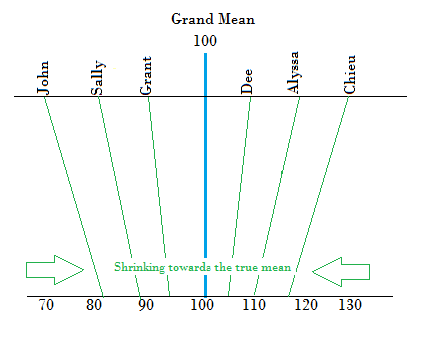
Shrinkage is where extreme values in a sample are “shrunk” towards a central value, like the sample mean. Shrinking data can result in:
- Better, more stable, estimates for true population parameters,
- Reduced sampling and non-sampling errors,
- Smoothed spatial fluctuations.
However, the method has many disadvantages, including:
- Serious errors if the population has an atypical mean. Knowing which means are “typical” and which are “atypical” can be difficult and sometimes impossible.
- Shrunk estimators can become biased estimators, tending to underestimate the true population parameters.
- Shrunk fitted models can perform more poorly on new data sets compared to the original data set used for fitting. Specifically, r-squared “shrinks.”
In Bayesian analysis, shrinkage is defined in terms of priors. Shrinkage is where:
“…the posterior estimate of the prior mean is shifted from the sample mean towards the prior mean” ~ Zhao et. al.
Models that include prior distributions can result in a great improvement in the accuracy of a shrunk estimator.
What is a Shrinkage Estimator?
A shrinkage estimator is a new estimate produced by shrinking a raw estimate (like the sample mean). For example, two extreme mean values can be combined to make one more centralized mean value; repeating this for all means in a sample will result in a revised sample mean that has “shrunk” towards the true population mean. Dozens of shrinkage estimators have been developed by various authors since Stein first introduced the idea in the 1950s. Popular ones include:
- Lasso estimator (used in lasso regression),
- Ridge estimator: used in ridge regression to improve the least-squares estimate when multicollinearity is present,
- Stein-type estimators, including the “original” James-Stein estimator.
Other shrinkage methods include step-wise regression, which reduces the shrinkage factor to zero or one, least angle regression and cross-validatory approaches.
References:
Efron B, Morris C. Data analysis using Stein’s estimator and its generalisation. J. Am. Stat. Assoc. 1975;70:311–319
Horl, A.E., and Kennard, R.W. (1970). “Ridge Regression: Biased Estimation for Nonorthogonal Problems.” Technometrics. Vol. 12, No. 1, pp 55-68.
James, W., and Stein, C., (1961). “Estimation with Quadratic Loss.” Proceedings of the Fourth Berkeley Symposium, Vol. 1 (Berkeley, California: University of California Press), pp. 361-379.
Rolph, J.E., (1976). “Choosing…Estimators for Regression Problems.” Communication in Statistics- Theory and Methods. 5(9):789-802. January.
Stein C. (1956). “Inadmissibility of the usual estimator for the mean of a multivariate normal distribution“. Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability. Vol. 1. University of California Press; Berkeley, CA, USA: pp. 197–208
Zhao, Y., et. al (2010). “On Application of the Empirical Bayes…in Epidemiological Settings.” Int J Environ Res Public Health. 2010 Feb; 7(2): 380–394.
Published online Jan 28. doi: 10.3390/ijerph7020380.