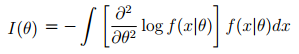Statistics Definitions > Fisher Information
What is Fisher Information?
Fisher information tells us how much information about an unknown parameter we can get from a sample. In other words, it tells us how well we can measure a parameter, given a certain amount of data. More formally, it measures the expected amount of information given by a random variable (X) for a parameter(Θ) of interest. The concept is related to the law of entropy, as both are ways to measure disorder in a system (Friedan, 1998).
Uses include:
- Describing the asymptotic behavior of maximum likelihood estimates.
- Calculating the variance of an estimator.
- Finding priors in Bayesian inference.
Finding the Fisher Information
Finding the expected amount of information requires calculus. Specifically, a good understanding of differential equations is required if you want to derive information for a system.
Three different ways can calculate the amount of information contained in a random variable X:
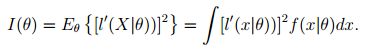
- This can be rewritten (if you change the order of integration and differentiation) as:
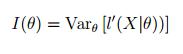
- Or, put another way:

The bottom equation is usually the most practical. However, you may not have to use calculus, because expected information has been calculated for a wide number of distributions already. For example:
- Ly et.al (and many others) state that the expected amount of information in a Bernoulli distribution is:
I(Θ) = 1 / Θ (1 – Θ). - For mixture distributions, trying to find information can “become quite difficult” (Wallis, 2005). If you have a mixture model, Wallis’s book Statistical and Inductive Inference by Minimum Message Length gives an excellent rundown on the problems you might expect.
If you’re trying to find expected information, try an Internet or scholarly database search first: the solution for many common distributions (and many uncommon ones) is probably out there.
Example
Find the fisher information for X ~ N(μ, σ2). The parameter, μ, is unknown.
Solution:
For −∞ < x < ∞:
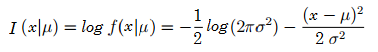
First and second derivatives are:
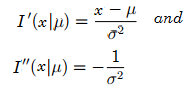
So the Fisher Information is:
![]()
Other Uses
Fisher information is used for slightly different purposes in Bayesian statistics and Minimum Description Length (MDL):
- Bayesian Statistics: finds a default prior for a parameter.
- Minimum description length (MDL): measures complexity for different models.
References:
Frieden and Gatenby.(2010). Exploratory Data Analysis Using FI. Springer Science and Business Media.
Friedan (1998). Physics from Fisher Information: A Unification. Cambridge University Press.
Lehman, E. L., & Casella, G. (1998). Theory of Point Estimation (2nd edition). New York, NY: Springer.
Ly, A. et. al. A Tutorial on Fisher I. Retrieved September 8, 2016 from: http://www.ejwagenmakers.com/submitted/LyEtAlTutorial.pdf.
Wallis, C. (2005). Statistical and Inductive Inference by Minimum Message Length. Springer Science and Business Media.