When a function is defined on a smaller set, it’s called a restriction. Reasons to restrict functions include:
- To formally define the domain of a function.
- To find an inverse function. For example, trigonometric functions do not have any restrictions, so there is no inverse. However, restricting the domain to a smaller interval allows you to work with inverse functions.
- To analyze segments that are “better behaved” with bounded variation, better modulus of continuity or monotonicity [1].
1. Restricting Domains to Define Functions
While many functions like the exponential function or cubed root function have no restrictions, others only work on specific sets. Therefore, their formal definitions include one or more restrictions. For example:
- Constant function: c is a real number (c ∈ ℝ),
- Linear function: m ≠ 0; In other words, the slope can’t equal zero, otherwise it turns into a constant function.
- Logarithm function: x > 0.
- Square root function: Restricted to x ≥ 0.
Restrictions of a function often happen because of some problem with algebra in the formula. For example, with rational functions, look out for places where the denominator would equal zero:

For radical functions, you can’t take square roots of negative numbers:
| Function | Restrictions |
| f(x) = √(x + 3). | x ≥-3 to avoid the problem of negative numbers. |
| f(x) = &radic(-x) | x ≥ 0. |
2. Restrictions of a Function to Find an Inverse
As an example, if you set an interval to [-π/2, π/2], the sine function becomes one to one [2]:
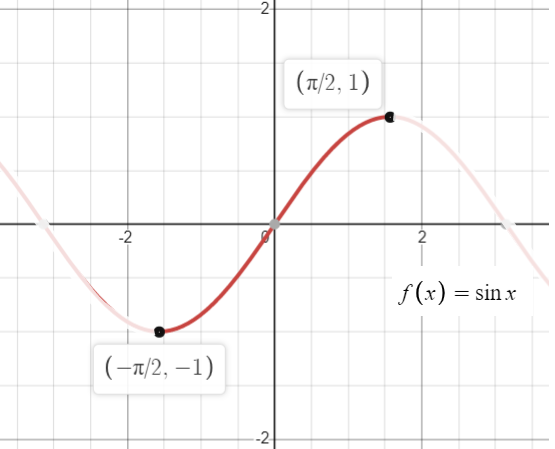
Switching the x and y values of the three coordinates (-π/2, -1), (0, 0), (π/2, 1) gives the inverse: (-1, -π/2), (0, 0), (1, π/2).
3. Restriction of a Function to make it “Better Behaved”
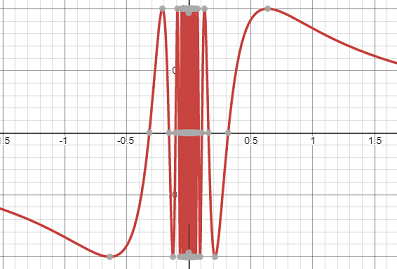
Some functions, like f(x) = sin(1/x), behave badly around x = 0. Because the function isn’t defined there, the values oscillate wildly and the function is almost impossible to work with. Restricting the domain to a smaller segment (one that doesn’t include zero!) means that the function is a little more workable.
References
Graph: Desmos.com
[1] Restrictions of continuous functions. Retrieved April 2, 2021 from: https://arxiv.org/abs/0711.0679
[2] Trigonometry With Restrictions. Retrieved May 2, 2021 from: https://www.alamo.edu/contentassets/35e1aad11a064ee2ae161ba2ae3b2559/trigonometric/math2412-inverse-trig-functions.pdf