Hypothesis Testing > Multiple Testing Problem
What is the Multiple Testing Problem?
If you run a hypothesis test, there’s a small chance (usually about 5%) that you’ll get a bogus significant result. If you run thousands of tests, then the number of false alarms increases dramatically. For example, let’s say you run 10,000 separate hypothesis tests (which is common in fields like genomics). If you use the standard alpha level of 5% (which is the probability of getting a false positive), you’re going to get around 500 significant results — most of which will be false alarms. This large number of false alarms produced when you run multiple hypothesis tests is called the multiple testing problem. (Or multiple comparisons problem).
Correcting for Multiple Testing
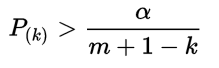
When you run multiple tests, the p-values have to be adjusted for how many hypothesis tests you are running. In other words, you have to control the Type I error rate (a Type I error is another name for incorrectly rejecting the null hypothesis). There isn’t a universally-accepted way to control for the problem of multiple testing.
Including:
- Single step methods like the Bonferroni correction and sequential methods like Holm’s method control the Family-wise Error Rate(FWER). The FWER is just a term for all of those false positives you get with multiple tests. Usually used when it’s important not to make any Type I Errors at all.
- The Benjamini-Hochberg procedure and Storey’s positive FDR control the False Discovery rate. These procedures limit the number of false discoveries, but you’ll still get some, so use these procedures if a small number of Type I errors is acceptable.
When Not to Control for Multiple Comparisons
An unfortunate “side effect” of controlling for multiple comparisons is that you’ll probably increase the number of false negatives — that is, there really is something significant happening but you fail to detect it. False negatives (“Type II Errors”) can be very costly (for example, in pharmaceutical research — where missing an important discovery can put research behind for decades). So if that’s the case, you may not even want to try to control for multiple comparisons. The alternative would be to note in your research results that there is a possibility your findings may be a false positive.
Multiple Comparisons for Non Parametric Tests
For non parametric tests, use the Bonferroni correction — which is your only viable option.