Statistics Definitions > Generalized Mean / Power Mean
What is the Generalized Mean?
The generalized mean (also known as the power mean or Hölder mean) is just a way of expressing most of the common means (like the arithmetic mean) in one formula:
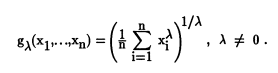
If you change λ (you’ll see this as p in some forms of the equation) to a particular value, you’ll get the formula for one of the common means:
- -1 : harmonic mean,
- 1 : arithmetic mean.
- 2: quadratic mean.
However, other real and hypothetical means are possible — in fact λ can be any non-zero number from -∞ to ∞. For values very close to zero (we’re talking a calculus limit here), the function approximates the geometric mean. Hypothetically, if you could put 0 in for λ, the equation would be the exact geometric mean, but as X0 = 1, a zero power wouldn’t work for this formula.
Getting into more technical stuff, the generalized mean can be derived in a couple of different ways:
- Using least squares estimates from transformed data.
- From maximum likelihood estimates.
Weighted Generalized Mean / Power Mean
A weighted mean in math is where you multiply your separate scores by a weighting factor. For example, your final exam worth 100 points might have a weighting factor of .4 and individual tests might have a weighting factor of .1 (see What is a Weighted Mean? for a step by step example). The weighted gen. mean works in exactly the same way. The only difference between this formula and the formula shown in the first part of this article is the addition of wi, a weighting factor.
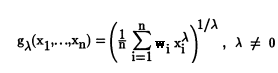
Note that the generalized mean is not the same thing as the Kolmogorov generalized mean, also called the quasi-arithmetic mean or generalized f-mean. Although they are similar in concept (i.e. they are both ways to fit one formula to a variety of means), they use different formulas to achieve this.
References:
Bullen, P. S. “The Power Means.” Ch. 3 in Handbook of Means and Their Inequalities. Dordrecht, Netherlands: Kluwer, 2003.