Familywise Error Rates > Holm-Bonferroni Method
You may want to read this article first: Familywise Error Rates.
What is the Holm-Bonferroni Method?
The Holm-Bonferroni Method (also called Holm’s Sequential Bonferroni Procedure) is a way to deal with familywise error rates (FWER) for multiple hypothesis tests. It is a modification of the Bonferroni correction. The Bonferroni correction reduces the possibility of getting a statistically significant result (i.e. a Type I error) when performing multiple tests. Although the Bonferroni is simple to calculate, it suffers from a lack of statistical power. The Holm-Bonferroni method is also fairly simple to calculate, but it is more powerful than the single-step Bonferroni.
Formula
The formula to calculate the Holm-Bonferroni is:
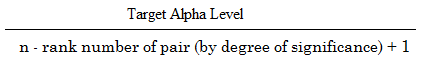
Where:
- Target alpha level = overall alpha level (usually .05),
- n = number of tests.
This next example shows how the formula works.
Example
Question: Use the Holm-Bonferroni method to test the following four hypotheses and their associated p-values at an alpha level of .05:
- H1 = 0.01.
- H2 = 0.04
- H3 = 0.03
- H4 = 0.005
Note: we already know the p-values associated with each hypothesis. If you don’t know the p-values, run a test for each hypothesis before attempting to adjust FWER using the Holm-Bonferroni method.
Step 1: Order the p-values from smallest to greatest:
- H4 = 0.005
- H1 = 0.01
- H3 = 0.03
- H2 = 0.04
Step 2: Work the Holm-Bonferroni formula for the first rank:
HB = Target α / (n – rank + 1)
HB = .05 / 4 – 1 + 1 = .05 / 4 = .0125.
Step 3: Compare the first-ranked (smallest) p-value from Step 1 to the alpha level calculated in Step 2:
Smallest p-value, in Step 1 (H4 = 0.005) < Alpha level in Step 2 (.0125).
If the p-value is smaller, reject the null hypothesis for this individual test.
The p-value of .005 is less than .0125, so the null hypothesis for H4 is rejected.
Step 4: Repeat the HB formula for the second rank .
HB = Target α / (n – rank + 1)
HB = .05 / 4 – 2 + 1 = .05 / 3 = .0167
Step 5: Compare the result from the HB formula in Step 4 to the second-ranked p-value:
Second ranked p-value, in Step 1 (H1 = 0.01) < Alpha level in Step 2 (.0167).
The p-value of .01 is less than .0167, so the null hypothesis for H1 is rejected as well.
Step 6: Repeat the HB formula for the third rank.
HB = Target α / (n – rank + 1)
HB = .05 / 4 – 3 + 1 = .05 / 2 = .025
Step 7: Compare the result from the HB formula in Step 6 to the third-ranked p-value:
Third ranked p-value, in Step 1 (H3 = 0.03) > Alpha level in Step 6 (.025).
The p-value of .03 is greater than .025, so the null hypothesis for H3 is not rejected.
The testing stops when you reach the first non-rejected hypothesis. All subsequent hypotheses are non-significant (i.e. not rejected).
Reference:
Holm, S. 1979. A simple sequential rejective multiple test procedure. Scandinavian Journal of Statistics 6:65-70