Probability Distributions > Mixture Distribution
What is a Mixture Distribution?
Simply put, a mixture distribution is a mixture of two or more probability distributions. Random variables are drawn from more than one parent population to create a new distribution. The parent populations can be univariate or multivariate, although the mixed distributions should have the same dimensionality. In addition, they should either be all discrete probability distributions or all continuous probability distributions.
The distributions can be made up of different distributions (e.g. a normal distribution and a t-distribution) or they can be made up of the same distribution with different parameters. For example, the following image shows a mixture of three normal distributions (called a Gaussian Mixture Model), each with a different mean:
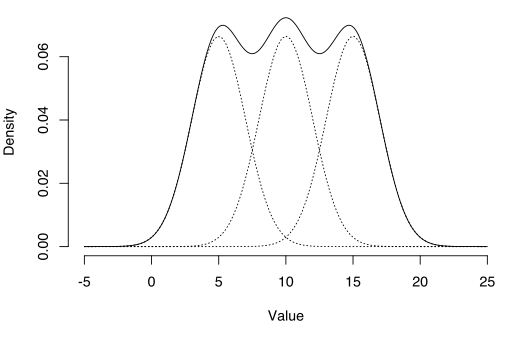
These new probability distributions are treated as bona fide probability density functions and so can be used to find expected values, maximum likelihood estimators and other statistics.
Examples of When to Use a Mixture Distribution
Mixture distributions are a useful way to show how variables can be differently distributed. Let’s say you are investigating how stress affects college exam scores. Two distributions that commonly represent the spread of scores in exams are the well-known bell curve (aka the normal distribution) and the bimodal distribution. You could have a .7 probability of your random variable following a bell curve and a .3 probability of it following a bimodal distribution (note that the probabilities must add up to 1).
Another example of when you might want to use a mixture distribution is when you have no idea what an outcome will be. For example, let’s say you are thinking of investing in stock for company XYZ. You think they are about to release a new gadget, which will make the stock rise dramatically by a mean of 100% with a standard deviation of 25%. However, there’s wind that the gadget might have major bugs, hindering a release. This would make the stock fall by a mean of 30% with a standard deviation of 15%. As you don’t know if the gadget is going to be released or not, the mixture will be an equally weighted (i.e. 50% for the falling distribution and 50% for a rising distribution).
More Formal Definitions
A random variable has a p1 chance of following a D1 distribution, a p2 chance of following a D2 distribution and a pn chance of following a Dn distribution, where “n” is the number of possible distributions. In the example above, we have two possible distributions, so:
- pbinomdal = .3
- Pnormal = .7
A mixture distribution can also be defined by the following formula:
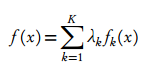
Where f1, f2,…fn are the component distributions and λk are the mixing weights (i.e. the probabilities for how much each individual distribution contributes to the mixture distribution).
- λk > 0,
- Σkλk = 1
Next: Specific example of a mixture distribution: The Beta-Binomial Distribution.