Contents (Click to skip to that section):
See also:
Parallel Boxplots
What is a Boxplot?
A boxplot, also called a box and whisker plot, is a way to show the spread and centers of a data set. Measures of spread include the interquartile range and the mean of the data set. Measures of center include the mean or average and median (the middle of a data set).
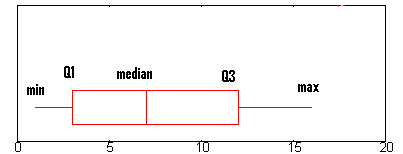
The box and whiskers chart shows you how your data is spread out. Five pieces of information (the “five number summary“) are generally included in the chart:
- The minimum (the smallest number in the data set). The minimum is shown at the far left of the chart, at the end of the left “whisker.”
- First quartile, Q1, is the far left of the box (or the far right of the left whisker).
- The median is shown as a line in the center of the box.
- Third quartile, Q3, shown at the far right of the box (at the far left of the right whisker).
- The maximum (the largest number in the data set), shown at the far right of the box.
How to Read a Box Plot
A boxplot is a way to show a five number summary in a chart. The main part of the chart (the “box”) shows where the middle portion of the data is: the interquartile range. At the ends of the box, you” find the first quartile (the 25% mark) and the third quartile (the 75% mark). The far left of the chart (at the end of the left “whisker”) is the minimum (the smallest number in the set) and the far right is the maximum (the largest number in the set). Finally, the median is represented by a vertical bar in the center of the box.
Box plots aren’t used that much in real life. However, they can be a useful tool for getting a quick summary of data.
How to Read a Box Plot: Steps
Step 1: Find the minimum.
The minimum is the far left hand side of the graph, at the tip of the left whisker. For this graph, the left whisker end is at approximately 0.75.
Step 2: Find Q1, the first quartile.
Q1 is represented by the far left hand side of the box. In this case, about 2.5.
Step 3: Find the median.
The median is represented by the vertical bar. In this boxplot, it can be found at about 6.5.
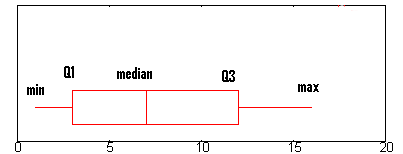
Step 4: Find Q3, the third quartile.
Q3 is the far right hand edge of the box, at about 12 in this graph.
Step 5: Find the maximum.
The maximum is the end of the “whiskers”: in this graph, at approximately 16.
Example 2
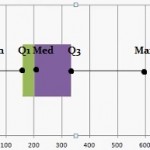
You can easily read a boxplot to find the five number summary. For example, the above image shows a box and whiskers chart with the following information:
- Minimum: 20
- Q1: 160
- Median: 200
- Q3: 330
- Maximum: 590
Exception: If your data set has outliers (values that are very high or very low and fall far outside the other values of the data set), the box and whiskers chart may not show the minimum or maximum value. Instead, the ends of the whiskers represent one and a half times the interquartile range (1.5*IQR).
All done. That’s how to read a box plot!
Note on Outliers:
Data sets can sometimes contain outliers that are suspected to be anomalies (perhaps because of data collection errors or just plain old flukes). If outliers are present, the whisker on the appropriate side is drawn to 1.5 * IQR rather than the data minimum or the data maximum. Small circles or unfilled dots are drawn on the chart to indicate where suspected outliers lie. Filled circles are used for known outliers.
Check out our YouTube channel for hundreds of basic statistics videos.
Back to Top
How to Make a Box and Whiskers Chart
Excel
Excel does not have a box and whiskers “Insert Graph” function, so you have to build one using stacked bar charts. This is a little more time-consuming than inserting a simple graph, but it you will end up with a great looking box and whiskers graph.
Note: This is an advanced Excel technique, so if you are new to Excel you may want to watch the video, which has more information and visuals for each step to make a box and whiskers chart in Excel.
How to Make a Box and Whiskers Chart in Excel: Steps
Sample problem: Make a box and whiskers chart in Excel for the following data set: 25, 145, 145, 148, 178, 178, 198, 201, 222, 210, 565, 589, 485, 333, 358, 158, 257.
Step 1: Type your data into one column in an Excel worksheet. For this example, type your data into cells A1:A11.
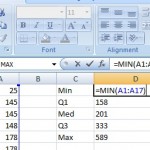
Step 2: Click an empty cell type “MIN, Q1, MED, Q3 and MAX” in a single column. In the next column over, type formulas for MIN, Q1, MED and MAX. The formulas are:
- =MIN(A1:A17)
- =QUARTILE(A1:A17,1)
- =MED(A1:A17)
- =QUARTILE(A1:A17,3)
- =MAX(A1:A17)
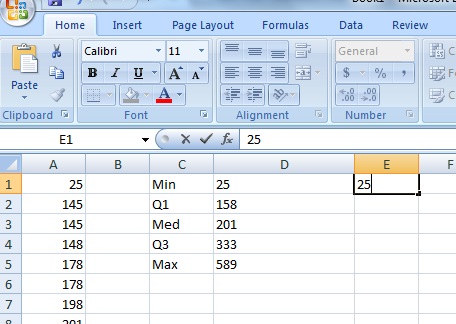
Step 3: In the next column over, type your Min (in this case, 25) into the cell next to the Min you calculated.
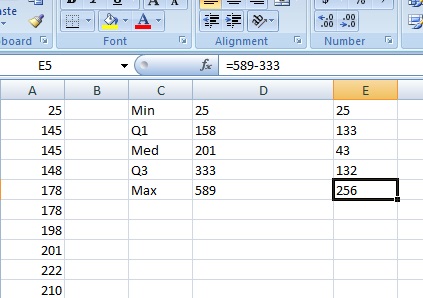
Step 4: Subtract each value in the previous column from the next value. In other words, subtract the Min from Q1, the Q1 from the Med, the Med from Q3 and Q3 from the Max.
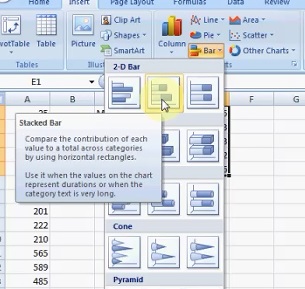
Step 5: Highlight the column of differences you calculated in Step 4, then click “Insert,” then click “Bar” and then click “Stacked Bar.”
Steps 6 – 10
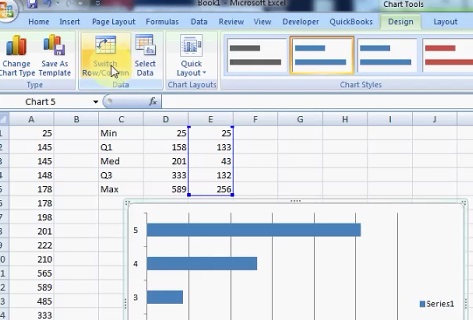
Step 6: Click the graph and then click the “Switch Row/Column” button.
Step 7: Select the left-hand blue box, right-click and then click “Format Data Series.”
Step 8: Click “Fill,” then click the “No Fill” radio button and then click “Close.”
Step 9: Add the whisker to the left-hand side using the following method:
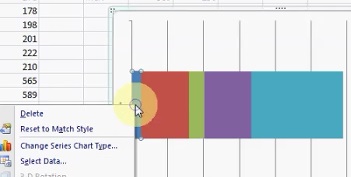
- Click the left-hand red box.
- Select the “Layout” tab, then click “Error Bars“. Next, click “More Error Bar Options.”
- Click “Error Bars with Standard Error.”
- Select the “Layout” tab again, then click “Error Bars” and then click “More Error Bar Options.”
- Click “Mins” and then type the difference between Q1 and the Min into the “Fixed Value” box. For this sample problem, that value is 133.
- Click “Close.”
- Remove the red color (fill) using the technique outlined in Steps 7 and 8 above.
Step 10: Add the whisker to the right-hand side of the box and whiskers chart Excel using the following method:
- Click the purple box.
- Select the “Layout” tab, then click “Error Bars” → “More Error Bar Options.”
- Click “Error Bars with Standard Error.”
- Select the “Layout” tab again, then click “Error Bars” → “More Error Bar Options.”
- Click “Plus” and then type the difference between Q3 and the Max into the “Fixed Value” box. For this sample problem, that value is 256.
- Click “Close.”
- Remove the light-blue color (fill) using the technique outlined in Steps 7 and 8 above.
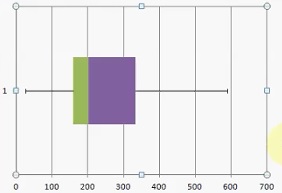
That’s it: You’ve created a box and whiskers chart in Excel!
Step 11: (Optional) Delete the “Series” information from the right: Click the name and then press the “Delete” key.
Tip: If you don’t see an error bar show up, that’s likely because you need to change the line color to “Black” from the More Error Bar Options window.
Check out our YouTube channel for more Excel help and tips!
TI 83 box plot: Overview
Let’s say you have a list of IQ scores for a gifted classroom in a particular elementary school. The IQ scores are: 118, 123, 124, 125, 127, 128, 129, 130, 130, 133, 136, 138, 141, 142, 149, 150, 154. That list doesn’t tell you much about anything. However, with a TI 83 box plot, the data can come to life.
Steps
You may find this article helpful if you’ve never entered a list into the calculator before: Entering lists on a TI 83.
Step 1: Press STAT, then ENTER, to edit list L1.
Step 2: Enter the data from the problem into the list (one value on each line, don’t enter the commas):
118, 123, 124, 125, 127, 128, 129, 130, 130, 133, 136, 138, 141, 142, 149, 150, 154.
Step 3: Press 2nd Y=, to access the Stat Plot menu.
Step 4: Press ENTER ENTER to turn on Plot1.
Step 5: Arrow down to Type, which has 6 icons to the right of it. Highlight the bottom middle icon, which looks like a syringe with two plungers, and press ENTER to select it.
Step 6: Make sure the XList entry reads “L1“. If it doesn’t, arrow down to it, Press Clear 2nd 1.
Step 7: Press Graph. You should see your Box plot.
Tip: If when you press Graph, you see the message “Err: Stat”, or you just don’t see a box plot like you expect to, then press Window, and try different settings. Especially try changing the Xscl (X Scale) item to a larger value.
TI-89
Example problem: Create a box and whiskers chart with the following data: 100, 340, 400, 350, and 400.
Step 1: Create a new folder called “Box.” From the HOME screen, press F4 and scroll down to NewFold (option B). Press ENTER.
Step 2: Press 2nd Alpha ( – x to spell B O X and press ENTER.
Step 3: Press APPS, then scroll down to Stats/List Editor. Press ENTER twice.
Step 4: Press the down arrow key to get to the first line of the list. Enter your data into list1. Follow each entry with a comma: 100, 340, 400, 350, 400.
Step 5: Press F2 then 1 to enter Plot Setup.
Step 6: Press F1, right arrow, and 5 to select mod box plot.
Step 7: Arrow down to Mark and select box.
Step 8: Arrow down and enter B O X (using the alphanumeric keypad) in the x. Press ENTER.
That’s it!
Back to Top
SPSS
SPSS allows you to create two types of boxplots: simple and clustered. Which type of boxplot you choose depends upon how many variables you want to plot. Choose the simple chart option when you want to create a plot of one variable, and choose the clustered boxplot option if you want to create a comparison of variable types. SPSS boxplots can be created in the Chart Builder or in the Legacy Dialogs menu.
Box plot in SPSS: Steps
Watch the video to see how to make a boxplot in SPSS using the Chart Builder, or read the steps below for a slightly different way to make a boxplot in SPSS, by using the legacy dialog.
Step 1: Open an existing worksheet with your data or type your data into a new worksheet.
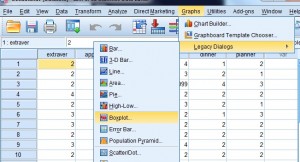
Step 2: Click “Graphs,” then click “Legacy Dialogs” and then click “Boxplot.”
Step 3: Click the type of chart you want to display, either Simple or Clustered, then click a radio button for either summaries of groups or separate variables.
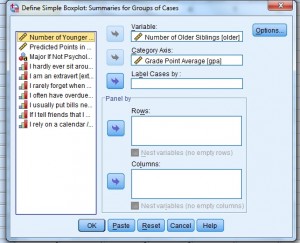
Step 4: Click “Define” to open the “Define Simple Boxplot” dialog box.
Step 5: Click a variable in the left window that you want to see medians or IQRs for. This is the analytical variable, the one that will be displayed on the y-axis. Click the top arrow to move the variable to the “Variable” window.
Step 6: Click a second variable in the left window that you want to display on the x-axis (the categorical variable), then click the second arrow down, to the left of Category Axis.
Step 7: Click “OK” to display the boxplot.
Minitab Box Plot
Thanks to Minitab’s easy-to-use graph creation software, you can make a box plot in Minitab in a couple of clicks. Watch this video on how to make a box plot in Minitab:
Step 1: Type your data into columns in a Minitab worksheet. Typically, you’ll want to type in two columns of data, one categorical and one quantitative (numerical).
Step 2: Click “Graph” on the toolbar and then click “Boxplot.”
Step 3: Choose a type of boxplot. If your data is in the form of column of quantitative data and one column of categorical variables (the most common scenario) then choose “One y” “With groups”.
Step 4: Click a variable name for your quantitative/numerical data and then click “Select” to move the item to the Graph Variables box.
Step 5: Click a variable name for your categorical data and then click “Select” to move that item to the Categorical Variables box.
Step 4: Click “OK” to create a boxplot.
That’s it!
Tips: Mouse over one of the boxes to display a window showing the median, Q1, Q3 and the IQR. You can also click on a number to bring up the Edit Scale box to specify labels, scales and other attributes for the boxplot.
References
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Wheelan, C. (2014). Naked Statistics. W. W. Norton & Company
Salkind, N. (2016). Statistics for People Who (Think They) Hate Statistics: Using Microsoft Excel 4th Edition.