Contents (Click to skip to that section):
What is Chebyshev’s Theorem?
Chebyshev’s theorem is used to find the proportion of observations you would expect to find within a certain number of standard deviations from the mean.
Chebyshev’s Interval refers to the intervals you want to find when using the theorem. For example, your interval might be from -2 to 2 standard deviations from the mean.
How to Calculate Chebyshev’s Theorem
Watch the video or read the steps below:
Formula
For normal distributions, about 68% of results will fall between +1 and -1 standard deviations from the mean. About 95% will fall between +2 and -2 standard deviations. The Theorem allows you to use this idea for any distribution, even if that distribution isn’t normal. The theorem states:
For a population or sample, the proportion of observations is no less than (1 – (1 / k2 ))
This holds as long as the z score’s absolute value is less than or equal to k.
When to Use the Formula
You can only use the formula to get results for standard deviations more than 1; It can’t be used to find results for smaller values like 0.1 or 0.9. Technically, you could use it and get some kind of a result, but those results wouldn’t be valid.
Example problem: a left-skewed distribution has a mean of 4.99 and a standard deviation of 3.13. Use the theorem to find the proportion of observations you would expect to find within two standard deviations from the mean:
Step 1: Square the number of standard deviations:
22 = 4.
Step 2: Divide 1 by your answer to Step 1:
1 / 4 = 0.25.
Step 3: Subtract Step 2 from 1:
1 – 0.25 = 0.75.
At least 75% of the observations fall between -2 and +2 standard deviations from the mean.
That’s:
mean – 2 standard deviations
4.99 – 3.13(2) = -1.27
mean + 2 standard deviations
4.99 + 3.13(2) = 11.25
Or between -1.27 and 11.25
That’s it!
Warning: As you may be able to tell, the mean of your distribution has no effect on the theorem! That fact can cause some wide variations in data, and some inaccurate results.
How to Calculate Chebyshev’s Formula in Excel.
Microsoft Excel has a wide variety of built-in functions and formulas that can help you with statistics. However, it does not have a built-in formula for Chebyshev’s Theorem. In order to calculate the theorem in Excel, you’ll need to add the formula yourself. If you want to use it just once or twice, you can type the formula into a cell. However, if you intend on using the formula several times, you can add a custom function (=CHEBYSHEV) to Microsoft Excel.
Temporary Use.
Step 1: Type the following formula into cell A1: =1-(1/b1^2).
Step 2: Type the number of standard deviations you want to evaluate in cell B1.
Step 3: Press “Enter.” Excel will return the percentage of results you can expect to find within that number of standard deviations in cell B1.
Adding a Custom Formula
Step 1: Open the Visual Basic editor in Excel. To open the Visual Basic editor, click the “Developer” tab and then click “Visual Basic.”
Step 2: Click “Insert” and then click “New Module.”
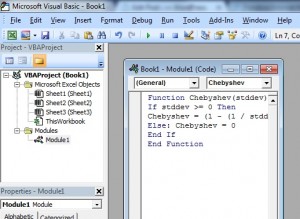
Step 3: Type the following code into the blank window:
Function Chebyshev(stddev)
If stddev >= 0 Then
Chebyshev = (1 – (1 / stddev ^ 2))
Else: Chebyshev = 0
End If
End Function
.
Step 4: Close the visual basic window and return to the worksheet. The custom function is now ready to use: type “=chebyshev(x)” into a blank cell, where “x” is the number of standard deviations. Excel will calculate Chebyshev’s theorem and return the result in the same cell.
Back to Top
Where did the Theorem Come From?
Pafutny Lvovich Chebyshev (1821-1894)was a Russian mathematician. His friend, mathematician and gifted linguist Irenée-Jules Bienaymé translated many of Chebyshev’s works into French.
In 1867 Chebyshev published a paper On mean values which first mentioned the inequality to give a generalized law of large numbers. However, the inequality actually first appeared fourteen years earlier in Bienaymés Considérations à l’appui de la découverte de Laplace. The editor who discovered Chebyshev’s use of Bienaymé’s inequality (without mention of the original author) said:
It is a pity that their common interest in the Inequality somehow “slipped through the cracks” in the early contacts between Bienaymé and Chebyshev. Possibly the Inequality was regarded by Bienaymé as a minor result compared with his main themes of linear least squares and Laplacian defence. Chebyshev’s recognition of its significance and its clear statement has, at any rate, always been a defensive point in his favour stressed by some historiographers. From The University of St. Andrews.
Chebyshev’s theorem is often spelled many different ways>you’ll find it spelled as Chebychev’s theorem, Chebyschev’s theorem and even Tschebyscheff’s theorem. That’s mostly due to the fact that his original name was Russian, which uses a different alphabet (cyrillic). “Chebyshev” is just the word, taken as it sounds and translated into an English approximation.
Fun fact: There is a crater on the moon named after him: Crater Chebyschev.
Back to Top
Chebyshev’s Inequality
Note: Technically, Chebyshev’s Inequality is defined by a different formula than Chebyshev’s Theorem. That said, it’s become common usage to confuse the two terms; A quick Google search for “Chebyshev’s Inequality” will bring up a dozen sites using the formula (1 – (1 / k2)). If you’re in a beginning stats class, pretty much the only form of Chebyshev’s formula you’ll be dealing with is that one.
For disambiguation, here’s the “other” inequality, which is mainly used to prove the Law of Large Numbers and other academic exercises. This is not the inequality used in elementary statistics. For that one, see Chebyshev’s Theorem above.
Chebyshev’s Inequality gives an upper bound to the probability that the absolute deviation of a random variable from the mean will exceed a stated amount. The formula reads as follows:
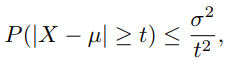
Applications of Chebyshev’s Inequality
The formula was used with calculus to develop the weak version of the law of large numbers. This law states that as a sample set increases in size, the closer it should be to its real mean (i.e. the one you would expect to see in a population). A simple example is that when rolling a six-sided die, the probable average is 3.5. A sample size of 5 rolls may result in drastically different results. Roll the die 20 times; The average should begin approaching 3.5. As you add more and more rolls, the average should continue to near 3.5 until reaching it. Or, it becomes so close that they are pretty much equal.
Another application is in finding the difference between the mean and median of a set of numbers. Using a one-sided version of Chebyshev’s Inequality theorem, also known as Cantelli’s theorem, you can prove the absolute value of the difference between the median and the mean will always be less than or equal to the standard deviation. This is handy in figuring out if a median you derived is plausible.
Chebyshev’s inequality doesn’t provide good accuracy for lower bounds if the sample size is small. For large random samples, it’s much more useful. That said, as there aren’t any restrictions at all on the shape of the underlying probability distribution, it tends to be very weak. Therefore, it’s not used much at all outside of academia.
See also: Chebyshev’s Sum Inequality.
Related Definitions for the Theorem
Chebyshev’s theorem is a catch-all term for several theorems, all proven by Russian mathematician Pafnuty Chebyshev. They include:
- Chebyshev’s Theorem (as described above),
- Chebyshev’s sum inequality (used in calculus),
- Bertrand’s postulate (used in number theory),
- Chebyshev’s equioscillation theorem (used in numerical analysis).
Bertrand’s postulate
Bertrand’s Postulate is used in number theory. It has very few applications to stats and you probably won’t come across it in an elementary stats course. According to the University of Tennessee, it states that if n is an integer greater than 3, there is at least one prime between n and 2n-2. It can also be stated as
![]()
Chebyshev’s equioscillation theorem
The Chebyshev equioscillation theorem shows the pattern of a continuous function on a closed interval. You won’t come across this theory in regular stats courses; It is used in numerical analysis courses at the graduate level and involves a somewhat complicated proof.
Back to Top
References
Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 and 571, 2002.
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.