Chebyshev’s sum inequality (or Chebyshev’s order inequality)* is an algebraic inequality for real numbers. The inequality tells us that if you take two decreasing sequences (from any distribution):
a1 ≥ a2 ≥ a3 ≥ a4 ≥…≥ an
and
b1 ≥ b2 ≥ b3 ≥ b4 ≥…≥ bn,
then the following statement, written in terms of summation notation, is true:
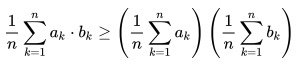
Similarly, it also tells us that if you reverse the sequences (i.e. make them increasing), then the inequality is also reversed:
a1 ≤ a2 ≤ a2 ≤ a2 ≤…≤ an
and
b1 ≤ b2 ≤ b2 ≤ b2 ≤… ≤ bn
and then the following statement is true:
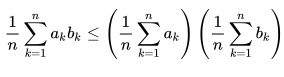 .
.
When two such sequences are equal, the inequality becomes the square of the inequality between the arithmetic mean and the root mean square (Besenyei. 2005).
The inequality is a very useful tool for investigating albebraic, geometric, and statistical problems; It is sometimes used in competitions like the Putnam.
Continuous Version of Chebyshev’s Sum Inequality
You don’t need to have a discrete series for Chebyshev’s sum inequality to be useful. There is also a continuous version, which tells us that if two real valued, integrable functions f and g are both non-increasing or both non-decreasing over the closed interval [0, 1].
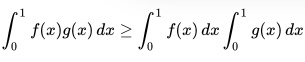
There’s one more version of this. If one of the functions is non-increasing and the other function is non-decreasing, simply reverse the inequality above.
The “Other” Chebyshev Inequality
Chebyshev’s sum inequality is a famous algebraic inequality often used in Olympiad style problems. It is named after the Russian mathematician Pafnuty Chebyshev, who lived between 1821 and 1894. There are actually two important inequalities named after him, so it is important not to get them mixed up.
In probability theory, the “Chebyshev Inequality” refers to an inequality that tells us how much date lies within a certain distance from the mean. See: Chebyshev’s Theorem.
Reference
Besenyei, A. Picard’s weighty proof of Chebyshev’s sum inequality. MAA MAthematics Magazine. Vol. 88, No. 1, February 2015.
*J. M. Steele, The Cauchy–Schwarz Master Class (An Introduction to the Art of Mathematical Inequalities),
Cambridge Univ. Press, NY, 2004
Inequalities. Retrieved from http://faculty.wwu.edu/sarkara/ph4.pdf on October 13, 2018.