Probability and Statistics > Famous Mathematicians
Famous Mathematicians
Many famous mathematicians have made notable contributions to the field of statistics, including.
Famous Mathematicians #1: George Boole.
George Boole was an English mathematician (1815-1864) best known for his work on logic, which became Boolean algebra, the math behind every computer. His early career was unremarkable: he didn’t study for a degree and became an assistant school teacher. Apart from some math lessons from his father, he was self-taught in mathematics. Some of his major accomplishments:
- He submitted many papers on differential equations and linear transformations to the new Cambridge Mathematical Journal, starting with “Researches on the Theory of Analytical Transformations” in 1839.
- In 1844 he was awarded the Royal Society’s first gold medal for mathematics, for a paper discussing the combining of algebra and calculus. He was elected as a fellow of the Royal Society on 1857.
- His 1847 “Mathematical Analysis of Logic” suggested that logic should be allied with math, not philosophy.
Despite having no degree, he was appointed professor of mathematics at Queen’s College in County Cork, Ireland. He did eventually receive honorary degrees from Oxford University and University College Dublin. His most important work is considered by many to be “An investigation into the Laws of Thought”.
Boolean algebra is the foundation for many parts of probability theory, including Bayesian statistics.
Famous Mathematicians and Statisticians #2: Pafutny Chebyshev.
Pafnuty Chebyshev (1821-1894) is a Russian mathematician who is well known for Chebyshev’s Theorem, which extends the properties of normal distributions to other, non-normal distributions with the formula (1 – (1 / k2 )), as long as the distribution’s z score‘s absolute value is less than or equal to k and the standard deviation is more than 1.
The inequality was originally known as the Bienaymé-Chebyshev inequality after linguist Irenée-Jules Bienaymé, the author of the original theorem.
Career
Pafutny Chebyshev was born on 16 May 1821 in Okatovo, Kaluga Region, Russia and Died on 8 December 1894 in St Petersburg, Russia. Over the course of his career he produced many notable papers, including papers on statistics, calculus, mechanics and algebra. In 1847, he was appointed to the University of St Petersburg after submitting a thesis titled On integration by means of logarithms. In 1850, he was promoted to extraordinary professor at St Petersburg. Pafutny Chebyshev is perhaps the most famous Russian mathematician and is considered the father of modern Russian mathematics.
Contributions to Mathematics
Pafutny Chebyshev is probably most famous for the theorem that’s named after him. However, he did make several other notable mathematical contributions, including:
- The Chebyshev inequality which states that if X is a random variable with standard deviation σ, then the probability that the outcome of X is no less than a\σ away from its mean is no more than 1/a2.
- Chebyshev polynomials.
- Chebyshev Bias
His name has a variety of spellings, all derived from his original Russian-language name Пафну́тий Льво́вич Чебышёв. According to Princeton University Professor A. Chaney, his name is alternatively spelled Chebychev, Chebyshov, Tchebycheff or Tschebyscheff (the latter two are French and German transcriptions).
Fun fact: The moon crater Crater Chebyschev and the asteroid 2010 Chebyshev are named after him.
3. Famous Mathematicians and Statisticians: Leohnard Euler.
Euler’s number (e) is a special number named after Leonhard Euler, with a very important place in mathematics. The number’s first few digits are 2.7182818284590452353602874713527; it’s an irrational number, which means that you can’t write it as a fraction.
 Leonhard Euler (pronounced “oiler“) was a German mathematician born in Basel, Switzerland to pastor Paul Euler and his wife, Marguerite. After moving to Riehen, Germany as an infant, he spent most of his career in St. Petersburg and Berlin. Euler is well known for his copious contributions to every area of mathematics that existed at the time; he produced so much work that the St. Petersburg Academy continued to publish his work for more than 30 years after his death. Euler was married two times. He had 13 children, although eight died in early childhood. His powers of memory and concentration were renowned. For example, he could recite all 9,896 lines of the epic Latin poem the Aeneid by memory. Euler went blind in his later years but continued to produce a prolific amount of work.
Leonhard Euler (pronounced “oiler“) was a German mathematician born in Basel, Switzerland to pastor Paul Euler and his wife, Marguerite. After moving to Riehen, Germany as an infant, he spent most of his career in St. Petersburg and Berlin. Euler is well known for his copious contributions to every area of mathematics that existed at the time; he produced so much work that the St. Petersburg Academy continued to publish his work for more than 30 years after his death. Euler was married two times. He had 13 children, although eight died in early childhood. His powers of memory and concentration were renowned. For example, he could recite all 9,896 lines of the epic Latin poem the Aeneid by memory. Euler went blind in his later years but continued to produce a prolific amount of work.
Notable contributions by Leonhard Euler to Probability and Statistics
Although Leonhard Euler made dozens of profound contributions to every area of mathematics, he made few notable contributions that specifically falls into the area of statistics. Statistics wasn’t even recognized as a discipline until Euler was well into middle-age, around 1749. However, much of the work he did do has served as a basis for studies in probability and statistics. For example, he is noted for his work on Graeco-Latin squares (sometimes called Euler Squares), which are used in the design of experiments.
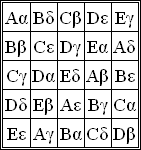
In the area of probability, Euler spent a large part of his mid-life studying the calculus of probability.
“…volume I.7 [of Opera Ominia, Euler’s published works] contains eight memoirs and a fragment concerning probability theory on finite sample spaces…the greatest portion of Euler’s writings on probability theory relate to the Genoese lottery” MAA.
Later in life, towards the end of the eighteenth century, Euler also worked on problems in the fledgling areas of mathematical statistics and observational error. For example, he contributed to the concept of maximum likelihood, where he showed that a carefully placed observation could destroy a well-built model.
Notable contributions to other areas of mathematics
Euler made hundreds of contributions to many areas of mathematics including applied mathematics, calculus, graph theory and number theory. Some of his best known work includes:
- The creation of Euler diagrams.
- The concept of a function (where every input is matched to exactly on output). He was the first to write the notation f(x).
- Euler’s number, e, the base of the natural logarithm.
- He introduced the use of the Greek letter Σ for summation notation.
- He popularized the use of the Greek letter π to mean the ratio of a circle’s circumference to its diameter although its use didn’t originate with him. The use of π originated with William Jones in 1706.
- He developed the power series and proved the power series expansion for e.
- He invented calculus of variations, including the Euler-Lagrange equation.
4. Famous Mathematicians and Statisticians: Carl Gauss.
Carl Gauss was born into poverty, but became one of the most influential mathematicians of all time.
As a child in elementary school, he was noticed as a prodigy in part because of his solution to a problem posed by his teacher: add up the numbers 1 to 100. Gauss noticed that 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101 and so on. The solution involves multiplying the number pairs (50) by 101 to get 5,050. This was written later, in more formal and general terms, as:
1 + 2 + ⋯ + n = n (n + 1) /2
Contributions to mathematics include:
- The Gaussian Distribution
- The Fundamental Theorem of Algebra
- The Method of Least Squares.
The Gaussian Distribution
The Gaussian distribution, also called the bell curve, is one of the most important concepts in probability and statistics. It was first developed by Carl Gauss.
Other Contributions to Math by Carl Gauss
Carl Gauss made contributions to almost every area of mathematics. The Fundamental Theorem of Algebra, where every algebraic equation has at least one solution, or root, is attributable to Gauss. He wrote it for his doctoral dissertation, which was published as Disquisitiones Arithmeticae (Inquiries into Arithmetic) in 1801.
Gauss is also famous for the method of least squares, which is used in regression analysis to fit a line to a series of data points.
One of his most interesting accomplishments was that he was the first mathematician to find a pattern in prime numbers: the pattern is a rough one: as the numbers increase by 1-, the probability of finding a prime number decreases by a factor of about 2. For example:
- The probability of finding a prime number from 1 to 100 is about 1 in 4.
- The probability of finding a prime from 1 to 1,000 is about 1 in 6.
- The probability of finding a prime from 1 to 10,000 is about 1 in 8
5. Famous Mathematicians and Statisticians: Gottfried Liebniz.
Liebniz is considered a forefather of modern logic and analytical philosophy. He is perhaps most well known in mathematics for developing calculus. He also worked on developing a practical counting machine which used the binary system, so arguably you could call him a grandfather of computing too. During development of the machine, he also laid the groundwork for probabilities and combinations but nothing was formally published in the field of probability theory. Although he did not formally publish anything on formal logic, he did develop in draft form some properties of sets, including: conjunction, disjunction, identity, and the empty set.
6. Famous Mathematicians and Statisticians: John Venn.
 John Venn (1834-1923) was a mathematician best known for his development of Venn Diagrams.
John Venn (1834-1923) was a mathematician best known for his development of Venn Diagrams.
Early Life and Career
John Venn was born in August 4th, 1834 in England, into a strict, evangelical family. His mother, Martha Sykes, died when Venn was a young boy. His father, Reverend Henry Venn, was rector of the parish of Drypool. There was never any doubt John Venn would enter the priesthood and although he received an early education, he had
“…… so slight an acquaintance with books of any kind that he may be said to have begun there his knowledge of literature.”
John studied at Gonville and Caius College at Cambridge University until 1857, when he received a degree in mathematics. Out of all the students who received first class (honors) degrees in mathematics, he placed sixth.
He was ordained as an Anglican priest in 1859 at the age of 25 but resigned from the priesthood several years later (in 1883), stating that Anglicism was incompatible with his philosophical beliefs. He became a fellow of the Royal Society and was awarded a Doctor of Science by Cambridge the same year. He Married Susanna Carnegie Edmonstone in 1868 and had one son, John Archibald Venn. In 1903 he was elected president of Gonville and Caius College.
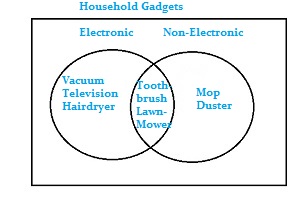
The Development of Venn Diagrams
Venn taught moral science, logic, and probability theory at Cambridge University, where he became a lecturer in 1862. It was during this time that he developed diagrams to illustrate set theory.
“I began at once somewhat more steady work on the subjects and books which I should have to lecture on. I now first hit upon the diagrammatical device of representing propositions by inclusive and exclusive circles. Of course the device was not new then, but it was so obviously representative of the way in which any one, who approached the subject from the mathematical side, would attempt to visualise propositions, that it was forced upon me almost at once.” ~ John Venn
Venn wrote several books, including Logic of Chance which was highly influential on the development of statistical theory. In that book, he stated that probability should be determined by forecasting how often something will happen, rather than “educated” assumptions. In his 1881 work, Symbolic Logic, Venn formally introduced the diagrams that would later bear his name.

Interestingly, John Venn was not the first person to develop the diagrams we now call Venn diagrams. Similar diagrams appeared almost two hundred years before Venn penned his work.
- Leonhard Euler used the diagrams as a teaching tool to explain Aristotle’s logic of the syllogism for a 15-year-old girl, which were published in Letters to a German Princess in 1768.
- Gottfried Leibniz’s almost identical diagrams appeared in logic papers he penned in 1686. However the papers were not formally published until 1903 (in De Formae Logicae Comprobatione per Linearum Ductus), long after Leibniz’s and Euler’s death.

Famous Mathematicians and Statisticians: References:
Bennet, D. Drawing Logical Conclusions.
Chaney, A. Pafnuty Chebyschev. Retrieved July 12, 2016 from: http://www.princeton.edu/~achaney/tmve/wiki100k/docs/Pafnuty_Chebyshev.html
Edwards, A. W. F. (2004). Cogwheels of the Mind: The Story of Venn Diagrams. JHU. p. 3. ISBN 9780801874345.
J J O’Connor and E F Robertson. John Venn.
MAA. Euler’s Analysis. Retrieved from: http://www.maa.org/press/periodicals/convergence/eulers-analysis-of-the-genoese-lottery-introduction July 12, 2016.
