Wald Test: Definition, Examples, Running the Test

What is the Wald Test?

wald test 2 — The Wald test can tell you which model variables are contributing something significant.

The Wald test (also called the Wald Chi-Squared Test) is a way to find out if explanatory variables in a model are significant. “Significant” means that they add something to the model; variables that add nothing can be deleted without affecting the model in any meaningful way. The test can be used for a multitude of different models including those with binary variables or continuous variables.

The null hypothesis for the test is: some parameter = some value. For example, you might be studying if weight is affected by eating junk food twice a week. “Weight” would be your parameter. The value could be zero (indicating that you don’t think weight is affected by eating junk food). If the null hypothesis is rejected, it suggests that the variables in question can be removed without much harm to the model fit.

If the Wald test shows that the parameters for certain explanatory variables are zero, you can remove the variables from the model.
If the test shows the parameters are not zero, you should include the variables in the model.

The Wald test is usually talked about in terms of chi-squared, because the sampling distribution (as n approaches infinity) is usually known. This variant of the test is sometimes called the Wald Chi-Squared Test to differentiate it from the Wald Log-Linear Chi-Square Test, which is a non-parametric variant based on the log odds ratios.

Comparison to Other Tests

The Wald test is a rough approximation of the Likelihood Ratio Test. However, you can run it with a single model (the LR test requires at least two). It is also more broadly applicable than the LRT: often, you can run a Wald in situations where no other test can be run.

For large values of n, the Wald test is roughly equivalent to the t-test; both tests will reject the same values for large sample sizes. The Wald, LRT and Lagrange multiplier tests are all equivalent as sample sizes approach infinity (called “asymptotically equivalent”). However, samples of a finite size, especially smaller samples, are likely to give very different results.

Agresti (1990) suggests that you should use the LRT instead of the Wald test for small sample sizes or if the parameters are large. A “small” sample size is under about 30.

Running the Test

Need help with a homework question? Check out our tutoring page!

The Wald Test statistic formula is:

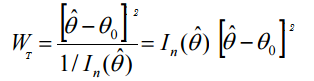
Where:

= Maximum Likelihood Estimator (MLE),
= expected Fisher information (evaluated at the MLE).

Basically, the test looks for differences: Θ⁰ – Θ. The general steps are:

Find the MLE.
Find the expected Fisher information.
Evaluate the Fisher information at the MLE.

With the combination of the MLE and Fisher information, the Wald test is very complex to work and is not usually calculated by hand. Many software applications can run the test.

Stata: use the test command.
R: see WALD test instructions for R (downloads a PDF) from the University of Toronto.
SAS: Use the TEST statement. WALD is the default if no test is specified.

Reference:
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.