Regression Analysis > Poisson Regression
What is Poisson Regression?
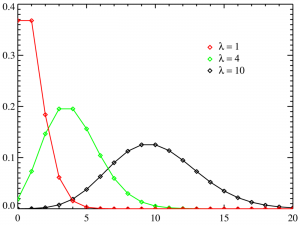
Poisson regression is used to model response variables (Y-values) that are counts. It tells you which explanatory variables have a statistically significant effect on the response variable. In other words, it tells you which X-values work on the Y-value. It’s best used for rare events, as these tend to follow a Poisson distribution (as opposed to more common events which tend to be normally distributed). For example:
- Number of colds contracted on airplanes.
- Number of bacteria found in a petri dish.
- Counts of catastrophic computer failures at a large tech firm in a calendar year.
- Number of 911 calls that end in the death of a suspect.
For large means, the normal distribution is a good approximation for the Poisson distribution. Therefore, Poisson regression is more suited to cases where the response variable is a small integer.
Poisson regression is only used for numerical, continuous data. The same technique can be used for modeling categorical explanatory variables or counts in the cells of a contingency table. When used in this way, the models are called loglinear models.
Assumptions
The assumptions for Poisson regression are:
- Y-values are counts. If your response variables aren’t counts, Poisson regression is not a good method to use.
- Counts must be positive integers (i.e. whole numbers) 0 or greater (0,1,2,3…k). The technique will not work with fractions or negative numbers, because the Poisson distribution is a discrete distribution.
- Counts must follow a Poisson distribution. Therefore, the mean and variance should be the same.
- Explanatory variables must be continuous, dichotomous or ordinal.
- Observations must be independent.
Running the Test
Poisson regression involves estimating the regression coefficients using maximum likelihood. These complex calculations aren’t usually performed by hand, but most statistical packages include a procedure.
- R: The classical Poisson uses a generalized linear model (GLM); use the glm() function in the stats package and the glm.nb() function in the MASS package.
- STATA: Use the Poisson command. From the menu: Statistics > Count outcomes > Poisson regression.
Reference:
Zeileis, A. Regression Models for Count Data in R. Retrieved September 9, 2016 from:
https://cran.r-project.org/web/packages/pscl/vignettes/countreg.pdf