Hypothesis Testing > Two Tailed Test
What is a Two Tailed Test?
This video explains the difference between one and two tailed tests:
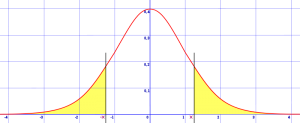
For example, let’s say you were running a z test with an alpha level of 5% (0.05). In a one tailed test, the entire 5% would be in a single tail. But with a two tailed test, that 5% is split between the two tails, giving you 2.5% (0.025) in each tail.
Need help with a homework question? Check out our tutoring page!
Two Tailed T Test
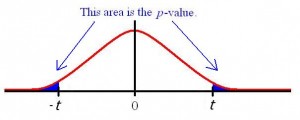
You may want to compare a sample mean to a given value of x with a t test. Let’s say your null hypothesis is that the mean is equal to 10 (μ = 10). A two tailed t test will test:
- Is the mean greater than 10?
- Is the mean less than 10?
If you choose an alpha level of 5%, and the f statistic is in the top 2.5% or bottom 2.5% of the probability distribution, then there is a significant difference in the means. That situation will also result in a p-value of less than 0.05. A small p-value gives you a reason to reject the null hypothesis.
Watch the video for an example of a two tailed z-test:
Two tailed F test
Watch the video for an example:
An f test tells you if two population variances are equal. A two tailed f test is the standard type of f test which will tell you if the variances are equal or not equal. The two tailed version of test will test if one variance is greater than, or less than, the other variance. This is in comparison to the one tailed f test, which is used when you only want to test if one variance is greater than the other or that one variance is less than the other (but not both).
Check out our YouTube channel for more stats help and tips!
References
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.