A nullcline is a point where a vector field changes direction [1]. The name means zero (null) slope (cline).
Nullcline in Differential Equations
In an autonomous system of two differential equations
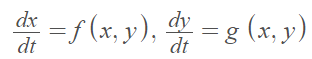
They can be defined as [2, 3]:
- x-nullcline: The set of points in the phase plane where dx/dt = 0. Geometrically, the vectors at these points are vertical (straight up and down). You can find the x-nullclines by solving f(x, y) = 0.
- y-nullcline: The set of points in the phase plane where dy/dt = 0. Geometrically, the vectors at these points are horizontal (moving to the left or right). You can find the x-nullclines by solving g(x, y) = 0.
If you have a different variable in your differential equations, the nullcline is called by that variable. For example, if you have dR/dt and dL/dt, then the curve where dR/dt = 0 is called the R null cline and the curve where dL/dt = 0 is called the L null cline.
Nullcline and Sketching Phase Planes
Nullclines are very useful for analyzing and sketching phase planes. The x-nullcline divides the phase plane into two regions where x moves in opposite directions. Similarly, the y-nullcline divides the phase plane into two areas where y either increases or decreases. Together, the x- and y-nullclines divide the phase plane into four regions [1]:
- x and y increase
- x and y decrease
- x increases and y decreases
- y increases and x decreases.
In the 2D plane, every point where the nullclines intersect is an equilibrium point.
Example
Example question: Find the x- and y- nullclines and the equilibrium point(s) for the following system of differential equations and sketch the result:
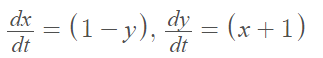
The nullclines happen when x′ = 0 or y′ = 0. Therefore, solve both equations for zero to get the nullclines:
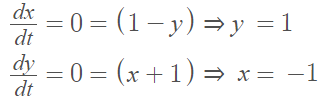
The following graph shows the solution:
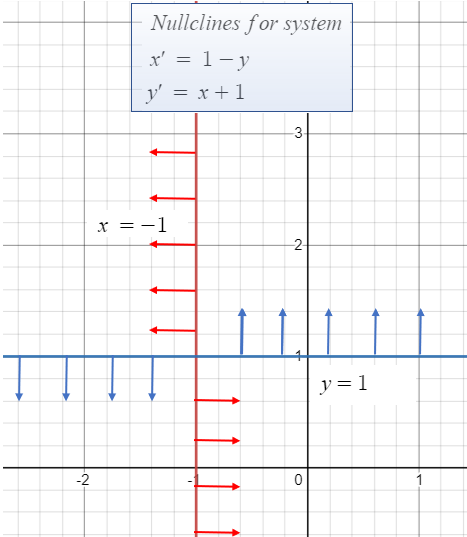
The vectors along the x-nullcline are vertical and along the y-nullcline they are horizontal; when a nullcline passes through the equilibrium point (-1, 1), the direction is reversed.
Although the nullclines are represented by lines in this example, they could technically be any curve.
References
[1] Izhikevich, E. (2007). Dynamical Systems in Neuroscience. MIT Press.
[2] Duke U. (2000). Systems of Differential Equations: Models of Species Interaction. Retrieved July 22, 2021 from: https://services.math.duke.edu/education/postcalc/predprey/pred3b.html
[3] A quick guide to sketching phase planes. Retrieved July 22, 2021 from: https://mcb.berkeley.edu/courses/mcb137/exercises/Nullclines.pdf