< Probability Distributions < Limiting Distribution
A limiting distribution, also called an asymptotic distribution, is the distribution of a sequence of random variables that converges to a particular distribution as the sample size increases. The term refers to the hypothetical distribution or convergence of a sequence of distributions; It is not a distribution in the general sense of the term, but rather a theory which aims to identify a limiting distribution for a series of distributions.
Some of these distributions are well-known. For example, the sampling distribution of the t-statistic will converge to a standard normal distribution if the sample size is large enough.
Sometimes the limiting probability distribution can be found by studying the behavior of cumulative distribution functions (CDFs) or probability density functions (pdfs). Theorems like Slutsky’s can also be used to explore convergence in probability distributions and may provide a limiting distribution.
Why do we need to find hypothetical distributions?
When you fit data to a model, it isn’t an exact science. Fitting data exactly to a known distribution is usually very difficult in real life due to limited sample sizes, resulting in a “best guess” based on what you know (or what your software knows) about behavior of large sample statistics.
The limiting/asymptotic distribution can be used on small, finite samples to approximate the true distribution of a random variable—one that you would find if the sample size was large enough.
Limiting probability distributions are important when it comes to finding appropriate sample sizes. When a sample size is large enough, then a statistic’s distribution will form a limiting distribution (assuming such a distribution exists).
One of the more common areas where limiting probability distributions show up is in the study of Markov Chains. As time n > ∞, a Markov chain has a limiting distribution π = (πj)j∈s. A value for π can be found by solving a series of linear equations.
Limiting Distribution and the CLT
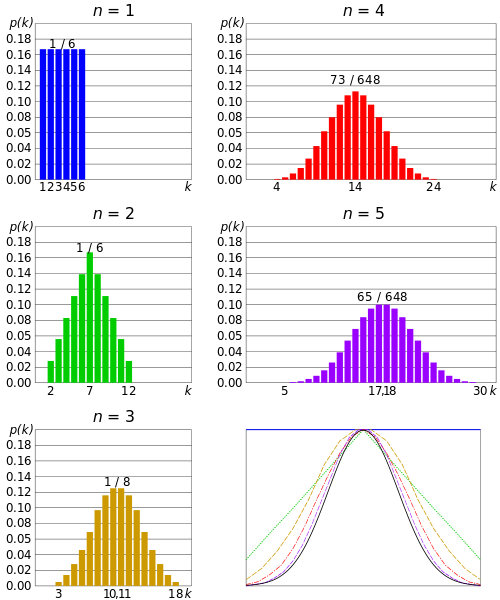
The Central Limit Theorem (CLT) uses the limit concept to describe the behavior of sample means. The CLT tells us that the sampling distribution of the sampling means approaches a normal distribution as the sample size increases — no matter what the shape of the population distribution.
What this is saying is, if you take more samples (especially large ones) the graph of the sample means will look more and more like a normal distribution, even if your graph is skewed or otherwise non-normal. In other words, the Limiting Distribution for a large set of sample means is the Normal Distribution.
Formal Definition
Epps [2] gives the term a more formal framework:
Suppose Xn is a random sequence with cdf Fn(Xn and X is a random variable with cdf F(x). If Fn converges to F as n > ∞ (for all points where F(x) is continuous), then the distribution of xn converges to x. This distribution is called the limiting distribution of xn.
In simpler terms, we can say that the limiting probability distribution of Xn is the limiting distribution of some function of Xn.
Limiting distribution uses
Limiting probability distributions are a powerful tool for making inferences about populations based on samples. They allow us to use known distributions to approximate the distribution of unknown quantities, such as the sample mean or the sample variance. Some of these distributions are well-known. For example:
- The t-statistic’s sampling distribution will converge to a standard normal distribution if the sample size is large enough.
- The central limit theorem states that the distribution of the sample mean converges to a normal distribution as the sample size increases. This means that we can use the normal distribution to approximate the distribution of the sample mean, even if the distribution of the population mean is not normal.
- The limiting probability distribution of the F statistic is given by the limiting distribution of the numerator [3].
In basic cases, an asymptotic distribution exists if the probability distribution of random variables Zi (i = 1, 2, …) converge to a probability distribution (the asymptotic distribution) as i increases The limiting probability distribution can sometimes be determined by analyzing the behavior of cumulative distribution functions (CDFs) or probability density functions (PDFs). Theorems such as Slutsky’s can be used to study convergence in probability distributions. A special case of a limiting distribution is found when a sequence of random variables is zero (Zi = 0) as i tends to infinity. In that case, the asymptotic distribution is a degenerate distribution, corresponding to the value zero.
Limiting distributions — stationary distributions that do not change over time — often show up in the study of Markov Chains. The limiting distribution represents the states of the chain as time approaches infinity. In other words, as time n > ∞, a Markov chain has a limiting distribution π = (πj)j∈s. To find the limiting distribution, solve the equation π = πP, where π is the initial distribution and P is the transition matrix. The transition matrix is a square matrix that provides the probability of moving from one state to another.
The limiting probability distribution does not always exist for Markov chains, but when it does, it predicts long-term Markov chain behavior. For example, the limiting distribution for a Markov chain that models the weather can predict future probabilities such as the likelihood of rain. As well as predictions, it can be used for understanding long-term patterns and designing algorithms for Markov chain problem-solving.
Advantages and disadvantages
Limiting distributions have many benefits for making reliable inferences about populations based on samples. For example, known distributions can approximate the distribution of unknown quantities, helping to decide whether a null hypothesis should be accepted or rejected as well as construct a confidence interval. When it comes to finding appropriate sample sizes, limiting probability distributions are important: the process in basic statistics involves taking a random sample of observations and fitting that data to a known distribution such as the normal or t distribution.
However, this isn’t an exact science since fitting data exactly to a distribution is difficult in real life due to limited sample sizes. Consequently, a “best guess” is made based on knowledge about large sample statistics. In such cases, the limiting or asymptotic distribution can be used on small, finite samples to approximate the true distribution of a random variable. Assuming such a distribution exists, when a sample size is sufficiently large, a statistic’s distribution will form a limiting distribution.
However, it is necessary to ensure that the conditions for a limiting distribution are satisfied for accuracy. Therefore, limiting distributions should be approached with awareness of their challenges, but their benefits cannot be overlooked.
References
- Photo credit:cmglee|Wikimedia Commons. CC By 3.0.
- Epps, T. (2013). Probability and Statistical Theory for Applied Researchers. World Scientific.
- Chapter 6: Asymptotic distribution theory. Retrieved May 20, 2023 from: https://www.bauer.uh.edu/rsusmel/phd/sR-9.pdf