Statistics Definitions > McNemar Test Example
What is the McNemar Test?
The McNemar test is a non-parametric test for paired nominal data. It’s used when you are interested in finding a change in proportion for the paired data. For example, you could use this test to analyze retrospective case-control studies, where each treatment is paired with a control. It could also be used to analyze an experiment where two treatments are given to matched pairs. This test is sometimes referred to as McNemar’s Chi-Square test because the test statistic has a chi-square distribution.
Assumptions for the McNemar Test
The three main assumptions for the test are:
- You must have one nominal variable with two categories (i.e. dichotomous variables) and one independent variable with two connected groups.
- The two groups in your the dependent variable must be mutually exclusive. In other words, participants cannot appear in more than one group.
- Your sample must be a random sample.
If your data does not meet these three assumptions, considering running another test for your data like a regular chi-square test.
Calculating the Test
In order to run a McNemar test, your data should be placed into a 2×2 contingency table, with the cell frequencies equaling the number of pairs. For example, a researcher is testing a new medication and records if the drug worked (“yes”) or did not (“no”). A table is set up with the count of individuals before and after being given the medication. The cell labels a-d are in blue:
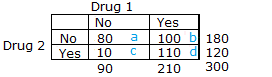
Cells b and c are used to calculate the test statistic; these cells are called “discordant.”
The McNemar test formula is:
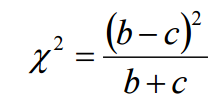
For the set of data above, we have:
= (100-10)2 / (100 + 10)
= 902 / 110
= 73.63
You have several options for calculating the McNemar test using technology, including:
- This online calculator will calculate the McNemar test using inputs for any 2×2 contingency table that you provide input for.
- SPSS: The binomial distribution is used for the McNemar test. You can find excellent instructions here on the SFU website.