Implicit Differentiation: Definition, Examples

Derivatives > Implicit Differentiation

Implicit differentiation is used to solve implicit expressions. Functions come in two flavors: explicit functions are in the form y = …. For example, y – 2x -5. This function could also be written as an implicit expression 2x – y = 5. While you could easily get this particular equation into an explicit form, sometimes it’s difficult, or impossible to solve for y;, which means you can’t use any of the “usual” methods of differentiation.

For example, the function 2xy = 1 can be easily solved for y, while a more complicated function, like 2y² -cos y = x² cannot.

With this technique, you directly differentiate both sides of the equation without solving for y. You’ll need to be comfortable with the chain rule, the power rule and various other techniques for finding derivatives.

Implicit Differentiation Examples

Example problem #1: Differentiate x = e^y using implicit differentiation.

Step 1: Rewrite the function, placing dy/dx on both sides:

Step 2: Differentiate the left side of the equation. The derivative of x is 1, so:

Step 3: Differentiate the right side of the equation. This example requires the chain rule:

Step 4: Use algebra to solve for y′.

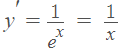
That’s it!

Finding the Derivative Implicitly: Example #2

In the above example, I used Leibniz notation for the derivative. In this next example, I use prime notation. The two notations mean the same thing (the derivative), but—as you’ll see in this example, y′ is a bit easier to write out and work with.

Example question #2: Find the implicit derivative of x³ + 4y² = 1.

Step 1: Find the derivative(s) for the left hand side.

For this example, there are two parts to find derivatives for: x³ and 4y²:

• x³ (the power rule) =
  3x
• 4y²:
  1. Differentiate with respect to y,
  2. Multiply by y′.

  Solution: 8yy′.

Combine the two answers from above (The Sum Rule):
3x + 8yy′

Step 2: Differentiate the right hand side. The derivative of a constant is 0.

Step 3: Put your answers from the left hand side (Step 1) and right hand side (Step 2) back together:

3x + 8yy′ = 0

This is the implicit derivative.