Statistics Definitions > T Statistic
What is a T Statistic?
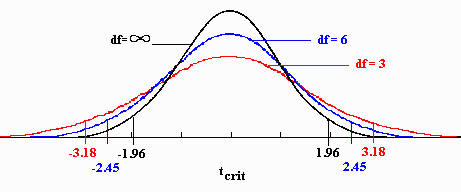
The T Statistic is used in a T test when you are deciding if you should support or reject the null hypothesis. It’s very similar to a Z-score and you use it in the same way: find a cut off point, find your t score, and compare the two. You use the t statistic when you have a small sample size, or if you don’t know the population standard deviation.
The T statistic doesn’t really tell you much on its own. It’s like the word “average” doesn’t mean anything on its own either, without some context. If I say “the average was 150,” it means nothing. If I say “the average weight of dogs seen in a veterinary office was 50lbs,” then the picture becomes clearer. In the same way, you need some more information along with your t statistic for it to make sense. You get this information by taking a sample and running a hypothesis test.
What is the T Statistic used for?
When you run a hypothesis test, you use the T statistic with a p value. The p-value tells you what the odds are that your results could have happened by chance. Let’s say you and a group of friends score an average of 205 on a bowling game. You know the average bowler scores 79.7. Should you and your friends consider professional bowling? Or are those scores a fluke? Finding the t statistic and the probability value will give you a good idea. More technically, finding those values will give you evidence of a significant difference between your team’s mean and the population mean (i.e. everyone).
The greater the T, the more evidence you have that your team’s scores are significantly different from average. A smaller T value is evidence that your team’s score is not significantly different from average. It’s pretty obvious that your team’s score (205) is significantly different from 79.7, so you’d want to take a look at the probability value. If the p-value is larger than 5%, the odds are your team getting those scores are due to chance. Very small (under 5%), you’re onto something: think about going professional.
T Score vs. Z-Score.
The Z-score allows you to decide if your sample is different from the population mean. In order to use z, you must know four things:
- The population mean.
- The population standard deviation.
- The sample mean.
- The sample size.
Usually in stats, you don’t know anything about a population, so instead of a Z score you use a T Test with a T Statistic. The major difference between using a Z score and a T statistic is that you have to estimate the population standard deviation. The T test is also used if you have a small sample size (less than 30).
T Statistic Formula
The statistic can be found in so many different ways, there is no single formula for it. The formula depends on what type of test you are trying to do. For example:
- One sample t test. This is the most common type of t test you’ll come across in elementary statistics. You can test the mean of a single group against a known mean. For example, the average IQ is 100. You can test a class of children with a mean score of 90 to see if that’s significant, or if it just happened by chance.
- A paired t-test compares means from the same group at different times (say, one year apart). For example, you could try a new weight loss technique on a group of people and follow up a year later.
It’s extremely unlikely you’ll want to calculate this statistic by hand. The math is complicated, tedious, time-consuming and prone to errors. Instead, you’ll want to use software like SPSS for Statistics or Excel for Statistics.
Need help with a homework question? Check out our tutoring page!
Check out our YouTube channel for more stats tips and help, including how to find T Statistics in Excel.
References
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Levine, D. (2014). Even You Can Learn Statistics and Analytics: An Easy to Understand Guide to Statistics and Analytics 3rd Edition. Pearson FT Press