Slutsky's Theorem: Definition

Slutsky’s theorem is used to explore convergence in probability distributions. It tells us that if a sequence of random vectors converges in distribution and another sequence converges in probability to a constant (not to be confused with a constant sequence), those sequences are jointly convergent in distribution. Basically, it allows you to use convergence results proved for one sequence for other closely related sequences.

Slutsky’s has no real practical applications; Its use is mostly limited to theoretical mathematical statistics (specifically, asymptotic theory). For example, it extends the usefulness of the Central Limit Theorem. Other uses include:

Explore convergence in functions of random variables.
Highlight critical properties of converging random variables.
Calculate the convergence of any continuous function of a set of statistics, providing that one set of those statistics converges (Davidson, 1994).

Formal Definition of Slutsky’s Theorem

More formally, Manoukian (1986) defines Slutsky’s theorem as follows:

If X_i be a random variable sequence that converges to a random variable X with a distribution function F(x) and if Y_i is a random variable sequence that converges to a probability of constant c. Then:

X_i + Y_i is distributed asymptotically as X + c.

X_i Y_i is distributed asymptotically as Xc.

X_i / Y_i is distributed asymptotically as X / c for c ≠ 0.

The theorem can also be written more succinctly as (from Proschan & Shaw, 2016):

Suppose that Xn→DX, An↠pA, and Bn↠pB,
where A and B are constants. Then AnXn+Bn↠DAX+B.

Simple Example

First, we need to define a couple of functions, g and h. The family of functions g_i, is defined as:

g₁({x_n}) = {x_n}
g₂({x_n}) = {2x_n}
g₃({x_n}) = {3x_n}
…
g_k({x_n}) = {kx_n}

g_i converges in probability to a constant c = μ.
And h is defined, in terms of g, as:
h (g₁, g₂, g₃…g_k) =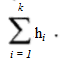

With reference to these two functions, Slutsky’s theorem tells us that the limit of h (g₁, g₂, g₃…g_k) as n approaches infinity is:
(k(k + 1) / 2) · μ
(Adapted from Kapadia et.al)

References:

Davidson, J. (1994). Stochastic Limit Theory: An Introduction for Econometricians.
Kapadia et. al. (2005). Mathematical Statistics With Applications.
Manoukian (1986) Mathematical Nonparametric Statistics. CRC Press.
Proschan, M. & Shaw, P. (2016). Essentials of Probability Theory for Statisticians. CRC Press.