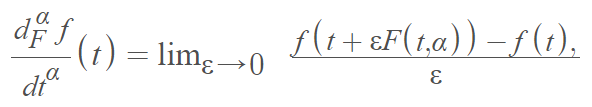The relatively new concept of a generalized derivative is an extension of the ordinary derivative to some classes of non-differentiable functions. Several generalizations of the nth derivative are obtained by one limiting process applied to one of the nth differences of f(x) [1].
The limiting process can be defined as follows [2]:
The generalized derivative of order 0 < α ≤ 1 of a real-numbered function f on a closed interval [a, b] is
Where F(α, t) is a positive, absolutely continuous function.
If the limit described above exists, then the function is α differentiable. Different local derivatives are particular cases of the kernel F(t, α).
The notation for the generalized derivative is a bar over the derivative [3]. For example, f ′(x) [3].
Types of Generalized Derivative
The collection of all generalized derivatives is the infinitesimal space. Some of the more common types of generalized derivative:
- Peano derivatives,
- A derivatives,
- Symmetric (Peano) derivatives,
- Symmetric Riemann derivatives,
- Symmetric quantum derivatives,
- Quantum symmetric Riemann derivatives.
There are a couple of different generalizations: Defining higher order derivatives via polynomial approximations, or as difference quotients [4].
The Peano derivative is an example of a generalized derivative that uses polynomial approximations. The first ordinary derivative and the Peano derivative have the same definition. However, the second derivatives (and higher) have different definitions. For example, the second Peano derivative is defined by [4]:
![]()
The nth symmetric Riemann derivative uses difference quotients instead of polynomial approximations. For example, consider the following:
![]()
If Δn is the nth symmetric difference, then the nth Riemann derivative is:
![]()
As a specific example of a generalized derivative, Dirac’s delta function is the second generalized derivative of the continuous function
![]()
References
[1] Haslam-Jones, U. (1953). On a Generalized Derivative. Retrieved August 6, 2021 from: https://academic.oup.com/qjmath/article-abstract/4/1/190/1568348?redirectedFrom=fulltext
[2] Zhao, D. and M. Luo. (2017) General conformable fractional derivative and its
physical interpretation, Calcolo, 54, 903-917
[3] Farassat, F. (1996). Introduction to Generalized Functions With Applications in Aerodynamics and Aeroacoustics. NASA Technical Paper 3428 from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.406.9810&rep=rep1&type=pdf
[4] Ash, J. Remarks on various generalized derivatives. Retrieved August 6, 2021 from: https://condor.depaul.edu/~mash/AshCalixtoGenDivSV.pdf