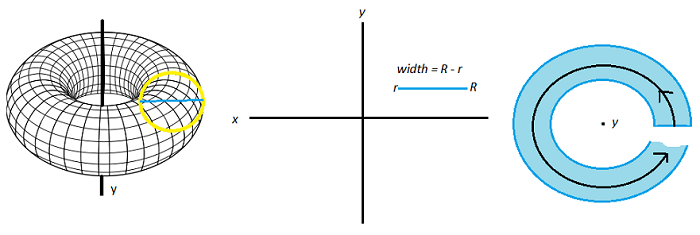
The washer method is a way to find the volume of objects of revolution. It’s a modification of the disc method for solid objects to allow for objects with holes. It’s called the “washer method” because the cross sections look like washers.
How to Use the Washer Method
In order to use this method, the axis of rotation must be perpendicular to the radius of rotation. You may need to integrate y with respect to x, depending on the orientation of your solid. Watch the video for an example or read on below:
You work the method in two stages:
- Calculate the volume of the solid, ignoring the hole,
- Find the volume of the hole and then subtract it.
This can be accomplished with the following integral:
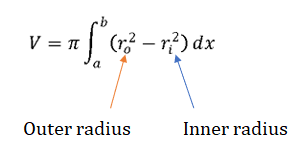
Example question: Find the volume of the solid of revolution bounded by y = x2 and y = x and rotated around the x-axis.
Step 1: Create a graph to help you visualize the problem. I used Desmos.com:
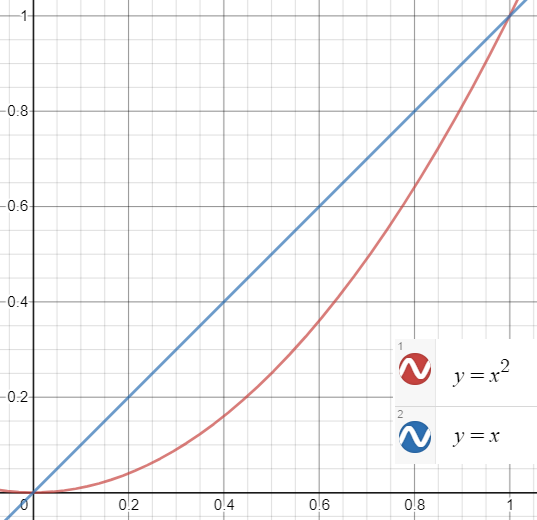
By looking at the intersections of the two functions, I can see that the two graphs form a leaf-like shape between x = 0 and x = 1. This is the shape we’re going to rotate. The interval from 0 to 1 is also the bounds of integration, which we’ll need to plug into the formula (i.e. from a to b).
Step 2: Sketch the solid of revolution. If you find visualizations tough, this is the most challenging step. One of the simplest ways to figure out the shape is to cut a piece of paper in the shape of the area (in this case, a leaf), then rotate it in your hands around a straw or stick. Or, you can do what I did: copy and paste the shape (in MS Paint), flipping it over the x-axis:
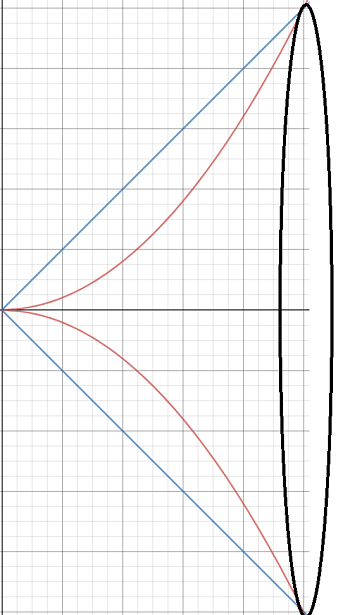
Step 3: Sketch in the washer. Here, you’ll need to decide if your washers will go along the x-axis or y-axis. This step is vital as it will determine which way you’re integrating (with respect to x, or y). For this example we’ll make washers traverse the x-axis:
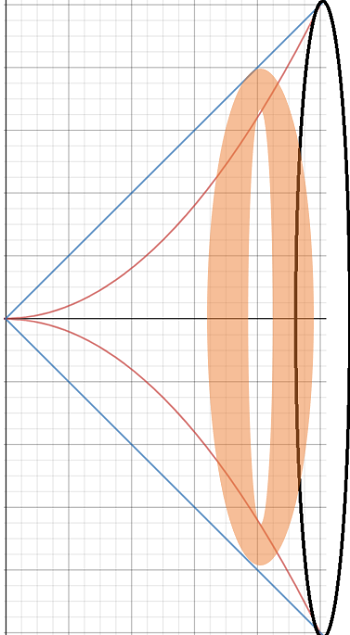
Try integrating with respect to x first (it’s often the easier option).
Step 4: Set up your integral. From the steps above, we have the following items to plug into the formula:
- r0 = x (the function y = x gives the radius for the outer washer)
- ri = x2 (the function y = x2 gives the radius for the outer washer)
- a = 0
- b = 1
Which gives:
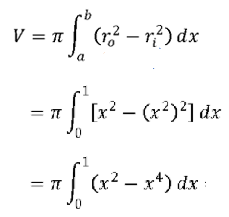
Step 5: Calculate the integral using your graphing calculator or an online integral calculator. I used the calculator at IntegralCalculator.com for the following steps:
- Apply linearity:

- Applying the integral rule for power functions to solve the integrals:

Step 6: Calculate the definite integral. We’re integrating from 0 to 1, so:
- Plug in x = 0 into the integral from Step 5 and solve
- Plug in x = 0 into the integral and solve
- Subtract the two numbers.
π((1/3)-(1/5)) – π((0/3)-(0/5)) ≈ 0.419
Note: Remember that volumes must be positive, so if you subtract the wrong way around (i.e. F(a) – F(b) instead of F(b) – F(a)), you’ll get a negative amount.