What is a Difference Quotient?
The difference quotient is one way to find a derivative or slope of a function. The formula is:
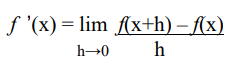
It might look intimidating, but it’s easier to solve than it looks, because many of the terms cancel out.
It’s called a “difference quotient” because the formula has two parts: a difference (subtraction) in the numerator and a quotient (division) between the two parts:
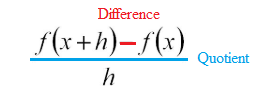
Watch the video for an overview and example:
Example
Find the difference quotient for the following function: f(x) = 3x + 2
Step 1: Insert your function into the first part of the formula. In this step, I’m replacing the “f(x+h)” in the left hand part of the numerator with the actual given function, 3x + 2:
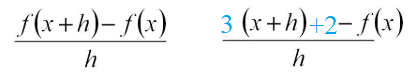
Essentially, I just changed the “x” part of 3x + 2 with “x + h”.
Step 2: Replace the “f(x)” in the formula’s numerator. This part is easy, because you’re just copying the formula exactly as written in the question and pasting it in:
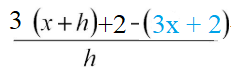
Step 3: Use algebra to simplify. In most cases, things will start to cancel out, making the formula a little less ugly.
For this particular formula, the first step of simplifying is to remove the parentheses, to get:
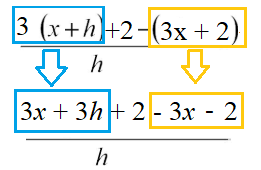
From here, you should be able to see that the following terms cancel out:
- 3x – 3x = 0
- 2 – 2 = 0
Leaving 3h / h = 3.
The difference quotient (aka the derivative or slope) is 3.
Origins of the Difference Quotient
The formula is derived from the “rise/run” slope formula you’re probably familiar with from algebra:
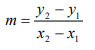
It’s the same formula, with a few substitutions. For example, instead of “y2” in the slope formula, you have “f(x + h)” in the difference quotient formula.
The full list of substitutions:
- f(x + h) → y2
- f(x) → y1
- x → x1
- x + h → x2
- h → change in x
- f(x + h) – f(x) → (y2 – y1)
Substituting those in to the slope formula, you get:
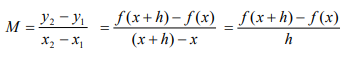
References
Difference Quotient. Retrieved October 13, 2019 from: https://www.csusm.edu/mathlab/documents/differencequotient-r6.pdf