Statistics Definitions > Within Mean Square
What is Within Mean Square?
Within Mean Square (WMS) is an estimate of the population variance. It is based on the average of all variances within the samples. Within Mean is a weighted measure of how much a (squared) individual score varies from the sample mean score (Norman & Streiner, 2008). The notation for within mean square error is MSwithin or you may sometimes see it written as:
![]()
Instead of σ the symbol for the population mean, you might also see “s” for the sample mean in the notation.
The most common formula is:
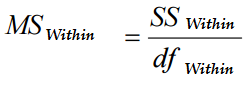
Where:
- “df” is the total degrees of freedom. To calculate this, subtract the number of groups from the overall number of individuals.
- SSwithin is the sum of squares within groups. The formula is: degrees of freedom for each individual group (n-1) * squared standard deviation for each group.
Need help with homework? Check out our tutoring page!
What is Within Mean Square used for?
Within Mean Square is used to calculate an F ratio in a one way ANOVA. The total sum of squares (SS) is the sum of both the within mean square and the between mean square (BMS). In a hypothesis test, the ratio BMS/WMS follows the shape of an F Distribution. If the ratio exceeds an F value for the test, it shows that there is a significant difference in your results.
Between vs. Within
The two terms sound similar, but there is a notable difference between the two terms.
Between group variation (sometimes called among group variation) is how much variation there is due to interaction between samples. The mean square between is therefore the mean square among sample means.
Within group variation is how much variation there is due to differences within individual samples, so the mean square within is defined as the mean square within samples.
References
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Norman, D. & Streiner, G. (2008) Biostatistics: The Bare Essentials. PMPH-USA.