Between Group Variation: Definition, Formula

Between group variation is used in ANOVA (analysis of variance) to measure variation between separate groups of interest. Unlike within group variation, where the focus is on the differences between a population and its mean, between group variation is concerned with finding how the means of groups differ from each other.

Between Group Variation Formula

The formula for between-group variation is:

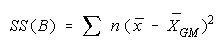
and is called the sum of squares between groups, or SS(B).

Σ is the summation symbol,
x = sample mean, (GM = group mean).

This measures the interaction between the groups or samples. If the group means don’t differ greatly from each other and the grand mean, the SS(B) will be small.

Note that for k groups, there will be k-1 degrees of freedom. The between groups variance is the variation, or SS(B), divided by its degree of freedom. We sometimes refer to the between groups variance as s_b ².

Between Group Variation, Within Group Variation, and the F-ratio

Between group variation is important in ANOVA because it is compared to within group variation to determine treatment effect.

We can calculate the “F-ratio” as (between group variation)/(within group variation). This is equivalent to (treatment effect + error)/(error). If the treatment effect goes to zero, the F ratio will be (error)/(error) and go to 1. If the treatment effect increases toward infinity, the F ratio will also go towards infinity.

References

Deater-Deckard et al. (2017). Within- and between-person and group variance in behavior and beliefs in cross-cultural longitudinal data. Journal of Adolescence. 62. 10.1016/j.adolescence.2017.06.002. Retrieved from https://www.researchgate.net/publication/317940722_Within-_and_between-person_and_group_variance_in_behavior_and_beliefs_in_cross-cultural_longitudinal_data on August 17, 2018.
Garbin, Cal. Between Groups and Within Groups ANOVA. Lecture Notes. Retrieved from http://psych.unl.edu/psycrs/941/q3/bg-wg.pdf on August 17, 2018.
Jones, James. Statistics Lecture Notes: One Way Anova.
Retrieved from https://people.richland.edu/james/lecture/m170/ch13-1wy.html on August 17, 2018.
Webb, Barbara. ANOVA – Analysis of Variance
Retrieved from http://homepages.inf.ed.ac.uk/bwebb/statistics/ANOVA1.pdf on August 17, 2018.