Contents:
Coefficient of Determination (R Squared)
The coefficient of determination, R2, is used to analyze how differences in one variable can be explained by a difference in a second variable. For example, when a person gets pregnant has a direct relation to when they give birth.
More specifically, R-squared gives you the percentage variation in y explained by x-variables. The range is 0 to 1 (i.e. 0% to 100% of the variation in y can be explained by the x-variables).
Watch this video for a short definition of r squared and how to find it:
The coefficient of determination, R2, is similar to the correlation coefficient, R. The correlation coefficient formula will tell you how strong of a linear relationship there is between two variables. R Squared is the square of the correlation coefficient, r (hence the term r squared).
Finding R Squared / The Coefficient of Determination
Need help with a homework question? Check out our tutoring page!
Step 1: Find the correlation coefficient, r (it may be given to you in the question). Example, r = 0.543.
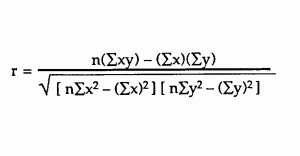
Step 2: Square the correlation coefficient.
0.5432 = .295
Step 3: Convert the correlation coefficient to a percentage.
.295 = 29.5%
That’s it!
Meaning of the Coefficient of Determination
The coefficient of determination can be thought of as a percent. It gives you an idea of how many data points fall within the results of the line formed by the regression equation. The higher the coefficient, the higher percentage of points the line passes through when the data points and line are plotted. If the coefficient is 0.80, then 80% of the points should fall within the regression line. Values of 1 or 0 would indicate the regression line represents all or none of the data, respectively. A higher coefficient is an indicator of a better goodness of fit for the observations.
The CoD can be negative, although this usually means that your model is a poor fit for your data. It can also become negative if you didn’t set an intercept.
Usefulness of R2
The usefulness of R2 is its ability to find the likelihood of future events falling within the predicted outcomes. The idea is that if more samples are added, the coefficient would show the probability of a new point falling on the line.
Even if there is a strong connection between the two variables, determination does not prove causality. For example, a study on birthdays may show a large number of birthdays happen within a time frame of one or two months. This does not mean that the passage of time or the change of seasons causes pregnancy.
Syntax
The coefficient of determination is usually written as R2_p. The “p” indicates the number of columns of data, which is useful when comparing the R2 of different data sets.
What is the Adjusted Coefficient of Determination?
The Adjusted Coefficient of Determination (Adjusted R-squared) is an adjustment for the Coefficient of Determination that takes into account the number of variables in a data set. It also penalizes you for points that don’t fit the model.
You might be aware that few values in a data set (a too-small sample size) can lead to misleading statistics, but you may not be aware that too many data points can also lead to problems. Every time you add a data point in regression analysis, R2 will increase. R2 never decreases. Therefore, the more points you add, the better the regression will seem to “fit” your data. If your data doesn’t quite fit a line, it can be tempting to keep on adding data until you have a better fit.
Some of the points you add will be significant (fit the model) and others will not. R2 doesn’t care about the insignificant points. The more you add, the higher the coefficient of determination.
The adjusted R2 can be used to include a more appropriate number of variables, thwarting your temptation to keep on adding variables to your data set. The adjusted R2 will increase only if a new data point improves the regression more than you would expect by chance. R2 doesn’t include all data points, is always lower than R2 and can be negative (although it’s usually positive). Negative values will likely happen if R2 is close to zero — after the adjustment, the value will dip below zero a little.
For more, see: Adjusted R-Squared.
Check out my Youtube Channel for more stats tips and help!
References
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.