Absolute Error & Mean Absolute Error (MAE)

What is Absolute Error?

Absolute Error is the amount of error in your measurements. It is the difference between the measured value and “true” value. For example, if a scale states 90 pounds but you know your true weight is 89 pounds, then the scale has an absolute error of 90 lbs – 89 lbs = 1 lbs.

This can be caused by your scale not measuring the exact amount you are trying to measure. For example, your scale may be accurate to the nearest pound. If you weigh 89.6 lbs, the scale may “round up” and give you 90 lbs. In this case the absolute error is 90 lbs – 89.6 lbs = .4 lbs.

Formula

The formula for the absolute error (Δx) is:

(Δx) = x_i – x,
Where:

x_i is the measurement,
x is the true value.

Using the first weight example above, the absolute error formula gives the same result:
(Δx) = 90 lbs – 89 lbs = 1 lb.

Sometimes you’ll see the formula written with the absolute value symbol (these bars: | |). This is often used when you’re dealing with multiple measurements:

(Δx) = |x_i – x|,
The absolute value symbol is needed because sometimes the measurement will be smaller, giving a negative number. For example, if the scale measured 89 lbs and the true value was 95 lbs then you would have a difference of 89 lbs – 95 lbs = -6 lbs. On its own, a negative value is fine (-6 just means “six units below”) but the problem comes when you’re trying to add several values, some of which are positive and some are negative. For example, let’s say you have:

89 lbs – 95 lbs = -6 lbs and
98 lbs – 92 lbs = 6 lbs

On their own, both measurements have absolute errors of 6 lbs. If you add them together, you should get a total of 12 lbs of error, but because of that negative sign you’ll actually get -6 lbs + 6 lbs = 0 lbs, which makes no sense at all — after all, there was a pretty big error (12 lbs) which has somehow become 0 lbs of error. We can solve this by taking the absolute value of the results and then adding:
|-6 lbs| + |6 lbs| = 12 lbs.

Need help with a homework question? Check out our tutoring page!

Absolute Accuracy Error

Absolute error is also called Absolute Accuracy Error. You might see the formula written this way:

E = x_experimental – x_true.
The formula is the exact same thing, just with different names. “x_experimental” is the measurement you take and x_true is the true measurement.

Mean Absolute Error

The Mean Absolute Error(MAE) is the average of all absolute errors. The formula is:

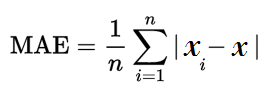
Where:

n = the number of errors,
Σ = summation symbol (which means “add them all up”),
|x_i – x| = the absolute errors.

The formula may look a little daunting, but the steps are easy:

Find all of your absolute errors, x_i – x.
Add them all up.
Divide by the number of errors. For example, if you had 10 measurements, divide by 10.

Absolute Precision Error

Absolute precision error is something completely different: it is the standard deviation of a set of measurements, given by the following formula:

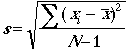
Where:

Σ = the summation symbol.
x_i is the i^th value (e.g. 1^st, 2^nd…),
x̄ = the sample mean,
N = the sample size.

References

Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.