A probability measure gives probabilities to a sets of experimental outcomes (events). It is a function on a collection of events that assigns a probability of 0 and 1 to every event, meeting certain conditions.
The role of a probability measure is to quantify the likelihood of each outcome from each event in the σ-algebra (a collection of sets that have certain properties); Simply put, σ-algebra assigns a probability to an event (e.g. “It will rain today”) and to that event’s complement (e.g. “It will not rain today”) and the union (“It will rain today, or it won’t”) [2].
Probability Measure Examples
For a roll of one six-faced die, the sample space (Ω) = {1, 2, 3, 4, 5, 6}. If A = {1, 3, 5} is the event that the roll is odd, then P(A) = ½.
Uniform Continuous Example: Let’s say you wanted to pick a random number between 0 and 1, where all numbers are equally likely. The sample space is the closed interval [0, 1]; The probability for any interval within [0, 1] is the length of I. Generally speaking, the uniform probability measure on [a, b] can be defined as [3]:
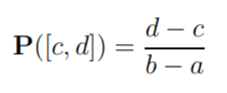
Formal Definition of Probability Measure
A probability measure P on F is a real-valued function P on F with three properties [2]:
- P(A) ≥ 0, for A ∈ F
- P(Ω) = 1, P(∅) = 0,
- For the disjoint sequence of events (i.e. Ai ∩ Aj = ∅ for i ≠ j) then:
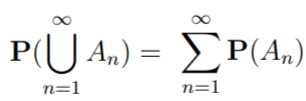
- ∅ = the empty set,
- ∩ = intersection,
- ∪ = union,
- Ac = complement (the set of outcomes in Ω which are not in A),
- ∈ = is an element of (is in the set),
- F = a collection of subsets of Ω
- σ-field = A collection of subsets of Ω is a σ-field if:
- Ω ∈ F
- A ∈ F → Ac ∈ F
- An ∈ F for n = 1, 2, 3, … ∪ (n = 1→∞) An ∈ F
Where:
References
[1] Probability. Retrieved March 11, 2021 from: https://cims.nyu.edu/~cfgranda/pages/DSGA1002_fall15/material/probability_1.pdf
[2] Kennedy, T. Probability measure and random variables. Retrieved March 11, 2021 from: https://www.math.arizona.edu/~tgk/mc/prob_background.pdf
[3] Probabilities. Retrieved March 11, 2021 from: https://www.math.arizona.edu/~tgk/464_10/chap1_8_26.pdf