Contents:
Order of Integration (Time Series)
You may want to read this article first: What is a Unit Root?
“Order of integration” is a summary statistic used to describe a unit root process in time series analysis. Specifically, it tells you the minimum number of differences needed to get a stationary series.
The Problem of Unit Roots

An ideal time series has stationarity. That means that a shift in time doesn’t cause a change in the shape of the distribution. Unit root processes are one cause for non-stationarity.
Order of Integration I(d)
If you have unit roots in your time series, a series of successive differences, d, can transform the time series into one with stationarity. The differences are denoted by I(d), where d is the order of integration. Non-stationary time series that can be transformed in this way are called series integrated of order k. Usually, the order of integration is either I(0) or I(1); It’s rare to see values for d that are 2 or more.
So, what exactly is an I(0) process?
An I(0) process is a non-integrated (stationary) process. Unfortunately, there’s no consensus on what exactly constitutes an integrated process, and what constitutes a non-integrated one. Burke & Hunter (2005) suggest that one way to view order of integration is “…being the number of unit roots in the autoregressive lag polynomial”.
Davidson, his paper, When is a Time Series I(0)?, states that “Since the inception of integrated time series modelling in econometrics, the question of what constitutes a non-integrated process has remained troublingly elusive.” He goes on to list no fewer than 5 different definitions from various sources, including:
-
- “A series with no deterministic component which has a stationary, invertible ARMA representation after differencing d times is said to be integrated of order d…(Engle and Granger 1987, p. 252.)”
and
- A finite (non-zero) variance stochastic process which does not accumulate past errors is said to be integrated of order zero…(Hendry 1995, p. 43).”
Davidson suggests that it may be easier think of an I(0) process as specific conditions that make asymptotic theory valid. That said, this simple definition does require some understanding of not-so-simple processes (like the concept of a limit in calculus and asymptotic theory). The definition is as follows:
A time series
![]()
is I(0) if the partial sum process XT, defined on the unit interval by
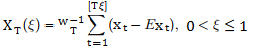
where ![]()
converges weakly to standard Brownian motion B as T → 1.
How to Find the Integration Order
The first step in transforming a time series is to see if you have a unit root process in the first place. Sometimes, a simple plot of the data will reveal the presence of a unit root (as in the image at the top of this article). However, looking at a plot — even one that obviously has a unit root — doesn’t give you the integration order. For that, you’ll have to perform further analysis. Two popular options are the KPSS test and the Augmented Dickey-Fuller test. For the AGF test, Dickey & Pantula (1987) suggest running the test assuming a higher order of integration (say, I(2))and working downwards to avoid the problem of over-differencing.
References:
Burke & Hunter. (2005). Modelling Non-Stationary Economic Time Series: A Multivariate Approach.
Davidson, J. When is a Time Series I(0)? In The methodology and practice of econometrics : a festschrift in honour of David F. Hendry. Oxford ; New York : Oxford University Press, 2009. Retrieved 8/13/2017 from: http://people.exeter.ac.uk/jehd201/WhenisI0.pdf
Dickey,D. & Pantula, S. (1987) Determining the order of differencing in autoregressive processes. Journal of Business and Economic Statistics. 5(4). 455-461.
Engle, R. F. and Granger, C. W. J. (1991) Long-run Economic Relationships: Readings in Cointegration, Oxford University Press.
Hendry, D. F. (1995) Dynamic Econometrics. Oxford: Oxford University Press.
Order of Integration (Integrals)
Order of Integration refers to changing the order you evaluate iterated integrals—for example double integrals or triple integrals.
Changing the Order of Integration
Changing the order of integration sometimes leads to integrals that are more easily evaluated; Conversely, leaving the order alone might result in integrals that are difficult or impossible to integrate.
You can change the order of integration—and get the same result— if the limits of all variables are constant. However, if you have variable limits of integration and you change the order of integration, you must also change the limits of integration (Ram, 2009). In visual terms, let’s say you have a double integral that involves a vertical strip, sliding along the x-axis. If you change the order, you then have a horizontal strip sliding along the y-axis.
Example
Example question: Compute the following double integral:

A quick glance at this integral reveals a problem: The “inside” integral (integrating with respect to x) requires you to find the antiderivative of 1/√(x3 + 1). There isn’t an integration rule that can help with that, so we’re going to switch the order of integration to find a solution.
Step 1: Write the limits of integration as inequalities:
- (0 ≤ y ≤ 1 )
- (√y ≤ x ≤ 1 )
Step 2: Find a new set of inequalities that describes the region with the variables in opposite order. Note: This step is much easier if you draw a graph of the area.
In the set of inequalities from Step 1, y came first. So first, define the region in terms of x instead.
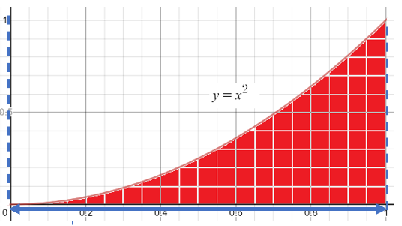
A quick look at the graph tells you that the area is bounded from the left and right by x-values ranging from 0 to 1, so we have:
(0 ≤ x ≤ 1)
Next, you’ll want to define the shape in terms of the y-variable; This is the area bounded from above and below. 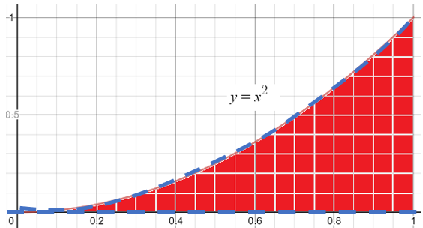
The area is bounded by the line y = 0 (i.e. the x-axis) on the bottom and the equation y = x2at the top, so:
(0 ≤ y ≤ x2).
The new set of inequalities, given that we are reversing the order of integration, is:
(0 ≤ x ≤ 1)
(0 ≤ y ≤ x2).
Step 3: Write the new integral with the inequalities from Step 2. Don’t forget to reverse “dx” and “dy”.

Step 4: Integrate as usual. For this double integral, you’ll need to integrate twice: once with respect to y, then with respect to x.
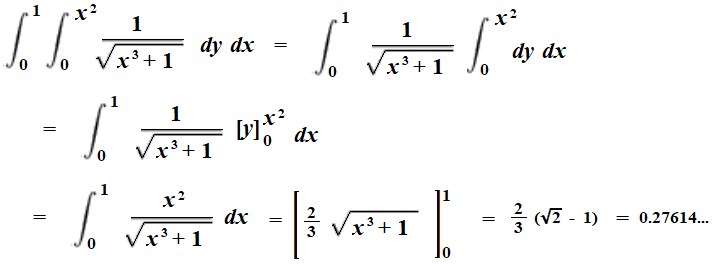
References
Ikenaga, B. Interchanging the Order of Integration. Retrieved July 3, 2020 from: http://sites.millersville.edu/bikenaga/calculus/interchanging-the-order/interchanging-the-order.html
Ram, B. Engineering Mathematics. Pearson, 2009.