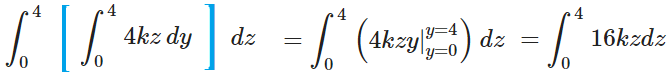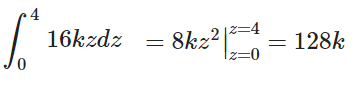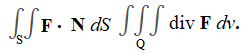Contents:
What is a Triple Integral?
The triple integral (also called the three-dimensional definite integral or volume integral) ∫∫∫Df(x, y, z) dV is an extension of the “usual” integral to three-dimensions. It is often the preferred choice for solving three-dimensional problems like finding center of mass, moments of inertia, or volume of a solid region.
Formal Definition of a Triple Integral
The definition of a triple integral is very similar to the double integral. A three-variable function f(x, y, z) over a three-dimensional domain V can be written as (Bronshtein et al., 2013):
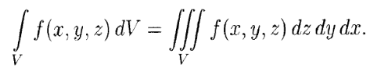
It isn’t as challenging as it looks, as long as you’re comfortable with the rules of integration. That’s because it’s iterated integrals: all you have to do is integrate three times, working in layers from the inside out.
Example
Example problem: Find the center of mass for a wooden block with side lengths of 4 m. One corner of the cube is positioned at the origin, with the adjacent corners on the positive x, y and z axes. Assume that the box’s density is proportional to the distance from the x-y plane and that k = 1 kg per cubic m per m.
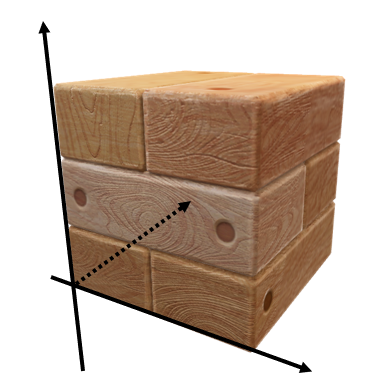
Solution
Step 1: Set up the triple integral.
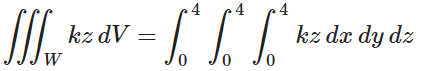
Here, W represents the cube, f(x, y, z) = kz is the density of the cube; k is a constant.
Step 2: Evaluate the integral. You’ll need to do this three times (once for each integral, with respect to x, y, and then z). Note: For a cube-like shape, the integral is independent of the order of integration, as long as f(x,y,z) is a continuous function.
- First, integrate with respect to x (treating y and z like constants):
As the lower limit is “0”, this makes for a fairly easy integration. Usually, you’ll have to evaluate the function at the lower and upper limits of integration, subtracting the two to get your area. However, as the lower bound (x = 0) will always equate to zero, you can basically skip that step and just plug in the value you found for the upper limit. - Evaluate the next layer (with respect to y):
- Evaluate once more and you’re done integrating!
You’re told that the block is measured in meters and that k is 1 kg per cubic m per m. So the mass of the block is 128 kg.
Divergence Theorem
The divergence theorem (sometimes called Gauss’s or Ostrogradsky’s theorem) is a connection between triple integrals and surface integrals. It states that under certain conditions, some volume integrals are equal to surface integrals. This can lead to simpler integration.
As a simple example, in order to perform integration on a shape like a pyramid, you would need four surface integrals: one for each side. But it’s possible, if the shape meets a few basic requirements, to use one triple integral instead.
Formal Definition of the Divergence Theorem
The theorem is valid for a closed surface S, meaning that S forms the complete boundary of the solid. Closed surfaces include regions bounded by cubes, ellipsoids, spheres, tetrahedrons, or combinations of those surfaces.
Formal Definition of the Divergence Theorem
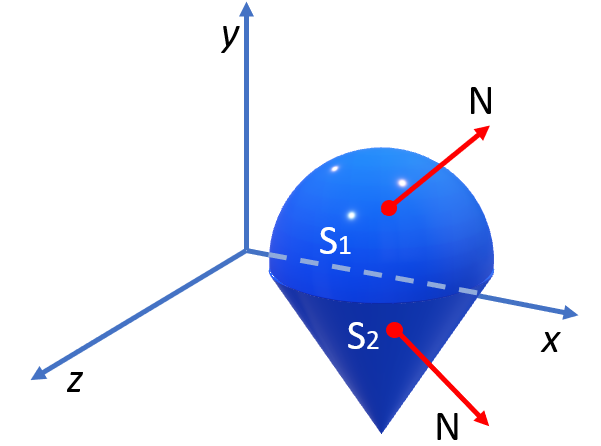
The above image shows an example of the type of shape the divergence theorem covers; A solid region, which we’ll call Q, bounded by a closed surface S and oriented by one or more unit normal vectors directed outward from Q.
If F is a vector field with component functions that have continuous first partial derivatives in Q, then [1]:
The theorem gets its name from the divergence of a vector field F = Mi + Nj + Pk. This is defined as:
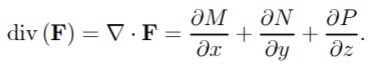
Where ∂ is a partial derivative.
Example
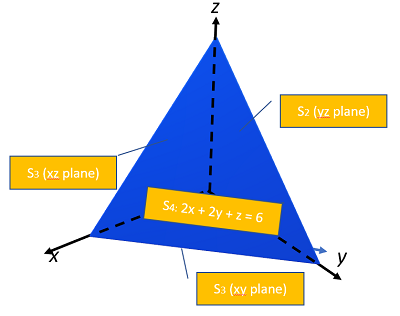
The above image is bounded by four planes: the coordinate planes x, y and the plane 2x + 2y + z = 6 with
F = xi + y2j + zk.
Instead of evaluating a surface integral for the four different planes, we can use a triple integral instead.
We need to find div F before we can solve the triple integral. We have:
- = 1 + 2y + 1
- = 2 + 2y.
I used Symbolab’s Calculator to evaluate the triple integral. The solution is:
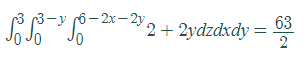
Divergence Theorem: References
[1] Larson, R. & Edwards, B. (2016). Calculus, 10th Edition. Cengage Learning.
Other References
Bronshtein, I. et al., Handbook of Mathematics. 2013. Springer Berlin Heidelberg.
Zill, D. & Wright, W. Calculus: Early Transcendentals. 2009. Jones & Bartlett Learning.