Sequence and Series > p-series
A p-series takes the form:
![]()
where p is a positive real number.
This notation represents an infinite sum, where n represents each natural number (whole, non-negative numbers that we use to count). In other words,
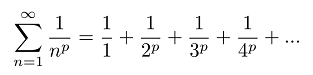
What is p-series Divergence?
Simply put, if a series diverges then it never settles (or sums to) a particular number. The harmonic series, where p=1, is divergent:
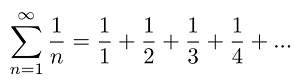
But how can we know whether other types converge or diverge?
The p-series test
A test exists to describe the convergence of all p-series. That test is called the p-series test, which states simply that:
- If p > 1, then the series converges,
- If p ≤ 1, then the series diverges.
Here are some examples of convergent series:
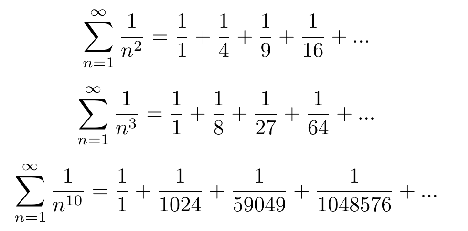
Note the “p” value (the exponent to which n is raised) is greater than one, so we know by the test that these series will converge.
Here’s are some examples of divergent series. Note that the exponents are all less than one:
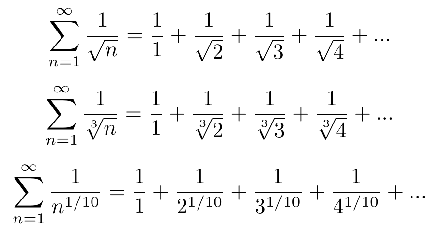
The p-series test is a great test for quickly finding convergence for this special series type. Even the harmonic series follows the test; The series diverges for p = 1.
Just make sure that the series you’re trying to evaluate follows the general formula. Important to note though, is that a p-series is not the same as a geometric series; While a p-series has the index (n) in the denominator of the fraction, a geometric series will have the index (n) in the exponent of the base. Here they are, side by side:
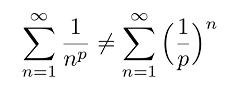
Also, the “p” is not short for power, as in power series, which has the basic form:
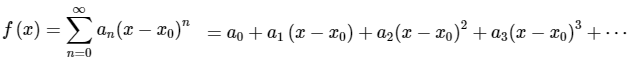
References
Benestad, C. et al. (2015). Power Series, Math 121 Calculus II. Retrieved January 3, 2020 from: https://mathcs.clarku.edu/~ma121/powerseries.pdf
Larson, R. & Edwards, B. (2013). Calculus. Cengage Learning; 10th edition