Contents:
What is an Infinitesimal?
In normal English, infinitesimal means “something that is extremely small”, but in mathematics it has an even stronger meaning. It is a quantity that is infinitely small; so small as to be non-measurable.
An infinitesimal is nonzero in size. In other words, it isn’t exactly zero. Despite it’s peculiarities, it still exhibits many of the properties of larger entities: properties such as angle or slope. These properties can be measured.
Infinitesimal Calculus
At the core of Calculus is the idea that, to really understand a curve, you have to understand what is happening at every instantaneous moment in time. That instant in time, when graphed on a curve, becomes an infinitely small interval—an infinitesimal. We call it a differential, and symbolize it as Δx. Summing up infinitely many infinitesimals gives us an integral.
Alternate Definition
The word has also, on occasion, been used to refer to functions which tend to zero. These are functions whose limits approach zero as the function approaches infinity.
History of Infinitesimal
The study of these infinitely small intervals is intrinsic to Calculus; in fact, Calculus has historically been known as ‘infinitesimal calculus’ or “the calculus of infinitesimals’. The word “calculus”, in that context, meant accounting or reckoning, and came from the name of a small counting pebble.
The study of infinitesimals began early; in fact, Archimedes, the Greek mathematician who lived from about 287 BC to 212 BC, gave the first logically rigorous definition of them. But they were not always well accepted. In fact, during the 17th century they were the subject of many political and religious controversies, and in 1632 there was actually a ban on infinitesimals issued by Roman clerics.
What Does dx Mean in Calculus?
The term “dx” means a small change in x.
More specifically, it’s an infinitesimal (really small!) change in two x-values written in Leibniz notation. We use it in calculus to analyze continuous functions, making the intervals between the x-values smaller and smaller—so small in fact, that the intervals are very close to zero.
Formally, dx is called the differential operator.
Dx in Derivatives
If you’ve studied limits in calculus, you’ll know that the limit is found by getting very close to an x-value.
For example, you might find the limit at x = 1 by looking at what happens when x = .999 or x = .99999. The dx notation describes this limiting procedure and it’s what we use to find derivatives.
You’ll see dx in various forms, including in this notation (d/dx) which means “take the derivative with respect to x.”
![]()
For example, if you see the following formula:
![]()
take the derivative of the function f(x) = 3x – 2.
What Does dx Mean in Calculus with a ∫?
When you see a ∫ and a dx, it means to integrate. The dx part of an integral tells you which variable to integrate; The x in dx tells you to integrate with respect to x. In other words, you’re trying to find the area under a curve by integrating along the x-axis.
Integrals have the basic notation ∫ f(x) dx:
- The function f(x) is the integrand—the function you’re integrating.
- The integral symbol ∫ and the dx are placeholders that say “integrate everything in between us.”
Some variations include du and dt. Usually these will match the integrand. For example ∫ u2 du.
- dt: Integrate with respect to t (time). Like x, this is usually along the x-axis and often appears in physics problems.
- du: Integrate with respect to u. The u here is a placeholder used un u-substitution or change of variables, both of which make finding certain types of integrals easier. You can think of the “u” as meaning unknown.
In multivariable calculus, the “dx” appears in the same position, along with dy and/or dz. When you see a double integral or a triple integral, this notation will tell you in which order you should integrate. For example, this double integral has “dx dy” at the end of the expression:
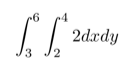
That’s telling you to integrate first with respect to x, then with respect to y.
What is Nonstandard Calculus?
Nonstandard calculus is the application of infinitesimals, using nonstandard analysis, to infinitesimal calculus.
Although infinitesimals had been around for some time (albeit barred from modern calculus), Robinson gave them a precise definition. He used the hyperreals (*R), an extension of real numbers to include infinitesimal numbers and infinite numbers. These numbers, which can be defined precisely, behave like very large natural numbers.
It’s important to note that the infinitesimal calculus of Newton and Leibniz and nonstandard calculus are not the same thing: nonstandard calculus is a relatively small field that applies nonstandard analysis to infinitesimal calculus.
Disambiguation note: Sometimes, the term “nonstandard calculus” is used to describe courses other than traditional college calculus, which has a different meaning entirely from the branch of calculus described here. For example, in the paper Revitalization of Nonstandard Calculus, Fetta (1996) the “nonstandard” calculus in question is actually business calculus.
Advantages and Disadvantages of Nonstandard Calculus
Nonstandard calculus is thought by many to be easier to understand, more intuitive, and conceptually simpler than the more common infinitesimal calculus approach. For example:
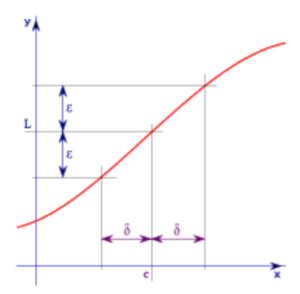
The definition of the continuity of a function at a point c is simply that x infinitely close to c implies that f(x) is infinitely close to f(c) (Sullivan, 2014).
However, others consider the formal structure of nonstandard calculus too technical for those without a good background in logic. Complicating the issue is that while real numbers are familiar and easy to understand, nonstandard reals are a challenge to comprehend for most students. That said, some courses have been developed that simplify these challenging details. Many are based on Jerome Keisler’s seminal works Elementary Calculus: An Infinitesimal Approach.
References
Fetta, I. (1996). Revitalization of Nonstandard Calculus. Retrieved May 14, 2020 from: https://files.eric.ed.gov/fulltext/ED417936.pdf
Krakoff, G. (2005). Hyperreals and a Brief Introduction to Non-Standard Analysis. Math 336. Retrieved May 14, 2020 from: https://sites.math.washington.edu/~morrow/336_15/papers/gianni.pdf
Sullivan, K. (2014). The Teaching of Elementary Calculus Using the Nonstandard Analysis Approach. The American Mathematical Monthly, Vol. 83, No. 5 (May, 1976), pp. 370-375.
Tuckey, C. (1993). Nonstandard Methods in the Calculus of Variations (Chapman & Hall/CRC Research Notes in Mathematics Series) 1st Edition. Chapman and Hall/CRC.
References
Keisler, Jerome. Foundations of Infinitesimal Calculus. Online Edition. Retrieved from https://www.math.wisc.edu/~keisler/foundations.html on December 6, 2018.
Stroyan, Kieth. A Brief Introduction to Infinitesiml Calculus. Retrieved from http://homepage.math.uiowa.edu/~stroyan/InfsmlCalculus/Lecture1/Lect1.pdf on December 6, 2018.