Contents (Click to skip to that section):
- Multivariate Function Definition
- What is Multivariable Calculus?
- The Multivariate Chain Rule
- Other Multivariable Calculus Tools and Definitions
1. Multivariate Function Definition
A multivariate function has several different independent variables. While “classroom” calculus usually deals with one variable, you’ll deal with their multivariate counterparts in applied sciences. While calculus commonly deals with functions with just one independent and dependent variable, multivariate functions are far more useful in everyday life. This is because most real-world processes depend on more than one parameter.
The functions we typically deal with have a single input and single output. “Input” and “output” refers to independent and dependent variables, typically denoted with x and y.
Notation
In calculus we write multivariate functions as having a dependent variable z and independent variables x and y:
z = f(x, y)
The inputs of a multivariate function the domain. The set of all possible outputs is the range.
2. What is Multivariable Calculus?
Multivariable calculus (also called multivariate calculus) deals with functions of several variables. Many techniques can be transferred from single variable calculus, including finding derivatives and integrals.
Multivariable calculus is a huge field that usually covers an entire semester, usually after at least one full year of single variable calculus.
Comparison of Single and Multivariable Calculus
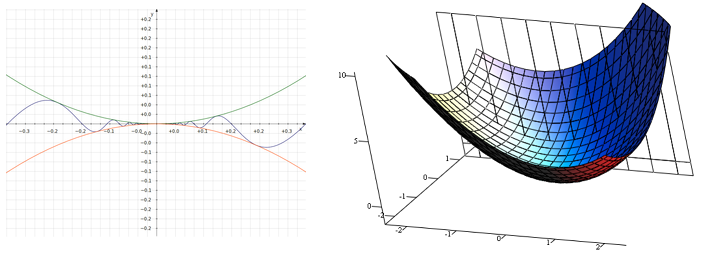
In single variable (univariate) calculus, the focus is on a function with a single input and a single output, like y = f(x). With multivariable calculus, more than one input is involved, such as z = x2 + y2.
You can also have multiple outputs, like:
- x = f(t),
- y = g(t),
- z = h(t).
While derivatives in single variable calculus give you a tangent line, in multivariate calculus the result is a tangent vector. The tangent vector is just your usual vector, extended to a 3-dimensional plane.
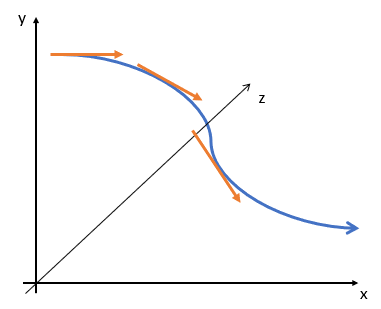
Another interesting difference is limits. In single variable calculus, you have a limit from the left and a limit from the right. When both of those limits exist and agree with each other, then we say there’s a limit. With multivariable calculus, this is a lot more challenging, because discontinuities don’t happen on a single line graph: they happen to 3D objects, which you can approach from multiple sides. Discontinuities are no longer simple broken lines, they often behave more like black holes in space, with the function sucked into (or blown out of) the point of discontinuity.

4. 3. The Multivariate Chain Rule
In the multivariate chain rule (or multivariable chain rule) one variable is dependent on two or more variables. The chain rule consists of partial derivatives.
For the function f(x,y) where x and y are functions of variable t, we first differentiate the function partially with respect to one variable and then that variable is differentiated with respect to t. The chain rule is written as:
![]()
Example
Let’s take a look at an example that shows how the chain rule works.
Example: The number of footballs a sporting goods store sells over time is x(t) t4 + 1; y(t) = 3t2 + 6 describes the price of footballs over time. Let z(t) = xy represent the revenue the store earns from the sale of footballs. How does revenue change with respect to time?
While there are several ways you could approach the solution, the easiest way to solve is to use the multivariate chain rule.
First, note that as a function of t, z is a function of a single variable. In this example, we have:
- Δ z / Δ x = y
- Δ z / Δ y = x
- dx/dt = 4t3
- dy/dt = 6t
Apply the chain rule formula from above to get the change in revenue over time:
dz/dt = (y)(4t3) + (x)(6t)
Other Multivariable Calculus Techniques and Definitions
Complex Analysis
Essential Singularity: Simple Definition, Examples
Harmonic Function
Iterated Integrals
Meromorphic Functions
Multivariate Gamma Function
Partial Derivative
Pole of a Function (Isolated Singularity)
Removable Singularity
Singularity Functions
Total Differential / Derivative
References
Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, p. 5, 2000.