Leibniz notation is a method for representing the derivative that uses the symbols dx and dy to designate infinitesimally small increments of x and y. It was introduced by German mathematician Gottfried Wilhelm Leibniz, one of the fathers of modern Calculus.
In Leibniz notation, the derivative of x with respect to y would be written:
![]()
The integral of f(x) is:
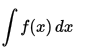
An Intuitive Understanding of Leibniz Notation
The derivative of f(x) can be defined by a limit:
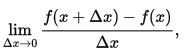
Where Δ x represents the difference in x. This, in turn, can be represented by
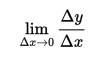
Leibniz saw this as the quotient of an infinitesimal increment of y by an infinitesimal increment of x. Accordingly, he wrote the above as:
![]()
Leibniz viewed an integral as the sum of infinitely many infinitesimal quantities f(x)dx. Since the Latin word for a mathematical sum is just summa, he chose to represent this special sum with a S; in particular, the elongated cursive style German S. Then he could use
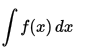
to mean an integral of f(x), summed over infinitely many dx.
History of Calculus Notation
Leibniz’s notation was not the only one used from the beginnings of Calculus. In fact, for some time, Isaac Newton’s notation was the most common. He wrote a his derivative with a dot above the x, like this.
![]()
Lagrange, another mathematician influential in the discovery of Calculus, used a prime (similar to an apostrophe). His derivative would look like:
![]()
In the end, Leibniz’s notation won out because of ease of use and ease of manipulation, but Lagrange’s notation is still used in some contexts and Newton’s notation can be seen in Physics applications.
References
Finan, Marcel B. Math 2243: Business Calculus. 2.3, Leibniz Notation of the Derivative. Retrieved from
https://faculty.atu.edu/mfinan/2243/business23.pdf on August 21, 2019.
McQuarrie, Barry. Barry McQuarrie’s Calculus II. Leibniz Notation for Derivatives. Retrieved from http://cda.mrs.umn.edu/~mcquarrb/teachingarchive/M1102/Resources/LeibnizNotation.pdf on August 21, 2019