Change of variable is a technique where, by a process of substitution, you can change the variables in an integral to new variables. Typically you would do this in an effort to simplify the problem, or make it easier to understand.
Simple Example of Change of Variable Techniques in Action
As an example, imagine you wanted to find the roots of a polynomial. You know all about how to solve quadratic polynomials—in fact, you’ve probably memorized a formula for it—but suppose this polynomial was something rather harder, say, a sixth degree polynomial. Suppose it was:
![]()
Sixth degree polynomials are not just hard to solve off the bat; often, they’re impossible. However, a change of variables can save the day. Let’s define a new variable, u = x3. Then you can write the equation as :
![]()
This is easier to solve, and you get:
![]()
Of course, you don’t actually want to know values of u; you want x. You can get that by substituting back, and you find the real solutions to the equation are:
![]()
Applications of Change of Variable
It’s not just solving polynomials where a technique like this comes in useful, though. Change of variable is also used in integration, differentiation, and coordinate transformations. When you are using it in Calculus, remember to change the variable every time it occurs to make a meaningful change. For differentiation, you could use the chain rule, for integration, you could use u substitution.
Imagine you wanted to use change of variable to solve the derivative:
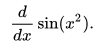
You can make up two new variables:
- y = sin u
- u = x 2.
Then you get:
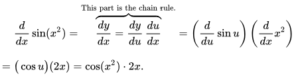
References
Penn State, Eberly College of Science. Stat 414/415: Probability Theory and Mathematical Statistics. Lesson 22: Functions of ONe Random Variable. Change of Variable Technique. Retrieved from https://newonlinecourses.science.psu.edu/stat414/node/157/ on August 20, 2019