A double point is a point on a curve where two branches of the curve intersect; in other words, it’s a point traced twice when a curve is traversed.
Types of Double Points
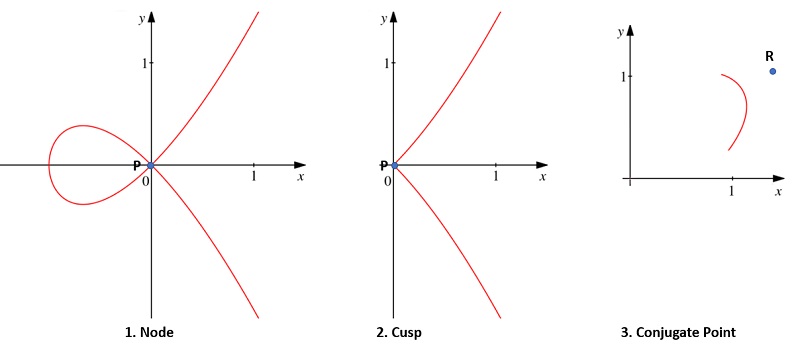
There are three types of double points:
- Node (also called an ordinary double point): a point where two branches of the curve intersect with different tangent line directions.
- Cusp (also called a stationary point or point of retrogression): a point where two real curve branches pass. The double tangent lines are real and coincide. As an example, the semicubical parabola ay2 (shown in the center of the above image) has a cusp at the origin with y2 the equation of the two tangent lines. Cusps are not always considered to be “true” double points [1].
- Conjugate Point: a point in the neighborhood of which there are no other real curve points. The tangent lines are usually imaginary. However, they can also be real.
Although the above definitions mention tangent lines, they do not define the nature of the double points. What’s important is the shape of the branches. That said, if you have two imaginary tangent lines, the double point must be a conjugate point. If there are two real, distinct tangent lines, that’s a node.
Multiple Points in General
A multiple point is where two or more tangents coincide [1]. Many different types of points are possible, called n-tuple points. For example, a point where three lines intersect is called a triple point [2]. In general, these points are defined as an interior point P of n (but no more than n) arcs such that any two arcs intersect at P.
The equations of the tangents at a multiple point (including double and triples) can be found by setting the lowest-degree terms in the curve’s Cartesian equation to zero with the origin at the multiple point [3].
References
[1] Kline, M. (1972). Mathematical Thought from Ancient to Modern Times: Volume 2.
[2] Rademacher, H. & Toeplitz, O. (1994). The Enjoyment of Math. Princeton University Press.
[3] James, R. & James, G. (1992). Mathematics Dictionary. Springer Netherlands.