The trapezoidal rule and Simpson’s rule are an approximate way to calculate the area under a curve (i.e. a definite integral). It’s possible to calculate how well these rules approximate the area with the Error Bounds formula.
The “error” is the difference between the actual “true” value and the approximation. Errors in the trapezoidal rule and Simpson’s rule can be calculated with a couple of straightforward formulas; These are useful when we want to increase the accuracy of an approximation. Increasing the number of partitions leads to better and better approximations: the following formulas give you a way to quantify those errors.
Errors in the Trapezoidal Rule and Simpson’s Rule: Formula
1. Error Bounds Formula for Trapezoidal Rule
The error formula for the trapezoidal rule is:
![]()
Where:
- a, b, = the endpoints of the closed interval [a, b].
- max|f′′(x)| = least upper bound of the second derivative.
- n = number of partitions (rectangles) used.
Example Question: What is the error using the trapezoidal rule for the function f(x) = x4 with 4 intervals on [0, 4]?
Solution:
Step 1: Calculate the second derivative: f′′ = 12x2. If the second derivative is not a continuous function, you cannot use the formula.
Step 2: Find the least upper bound (the “max”) of the second derivative on the interval (for this example, the interval is [0, 4]. You can do this in two ways:
- Look at a graph and locate the max on the interval, or
- Find the critical numbers and evaluate the function for those numbers (including at the endpoints).
Looking at a graph of f′′ = 12x2, we can see that the max value is f(x) = 192.
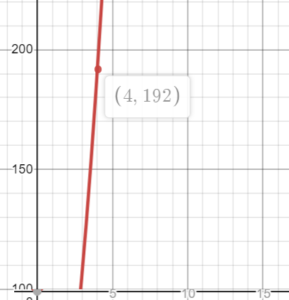
Step 3: Set up the formula and solve: Plugging in our numbers, we get:
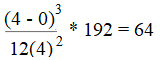
Where:
- a, b are given in the question as 0, 4,
- n = 4 (from the question)
- max|f′′(x)| = LUB from Step 3.
The error between the Trapezoid rule and definite integral is 64. Increasing the number of partitions “n” will result in better approximations.
2. Error Bounds Formula for Simpson’s Rule
The error formula for Simpson’s rule is similar. The main difference is that it uses the max of the fourth derivative f4:
![]()