What is the Stratonovich Integral?
The Stratonovich Integral, used in stochastic differential equations, is a way to integrate stochastic functions. It is defined as [1]:
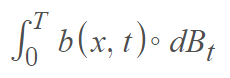
Stochastic differential equations deal with noise in physical processes. It is usually impossible to construct a continuous path white noise process; true white noise signals have flat Fourier spectrums, implying infinite energy [2]; The Stratonovich integral can interpret the noise term and create a workable model for noisy dynamics.
Stratonovich Integral vs. Itô integral
The Stratonovich integral preserves the chain rule, but this comes at an expense: unlike the Itô integral, it doesn’t have martingale properties. Matringales “have a lot of structure” and are very convenient to work with [3]. However, as the Itô integral “behaves dreadfully” under changes of coordinates, the Stratonovich integrals (which is not a martingale) is a viable alternative. That said, the Stratonovich is harder to work with due to its lack of martingale structure [4].
Both integrals are closely related to each other and can be calculated from each other; this makes it easy to switch from one integral to another. There is a rule of thumb for choosing one over the other:
- Choose the Stratonovich Integral if you are working with stochastic calculus on smooth manifolds. For example, if you’re constructing Brownian motion on manifolds, the differential equation of Cartan development (a rolling map of one surface over another) can be translated directly into a Stratonovich Integral.
- Choose the Itô integral if you want to model turbulence at small length scales [5].
References
[1] The Itô & Stratonovich integrals. Retrieved October 26, 2021 from: https://www.robots.ox.ac.uk/~lsgs/resources/ito-strat.pdf
[2] Van Kampen, N. G. ”Itô versus Stratonovich.” Journal of Statistical Physics 24.1 (1981): 175-187.
[3] Big picture concerning Ito integral, Stratonovich integral and standard results in probability theory. Retrieved October 26, 2021 from: https://mathoverflow.net/questions/22828/big-picture-concerning-ito-integral-stratonovich-integral-and-standard-results
[4] Stratonovich’s Theory. Retrieved October 26, 2021 from: http://www-math.mit.edu/~dws/ito/ito8.pdf
[5] The Azimuth Project. Stratonovich integral. Retrieved October 26, 2021 from: https://www.azimuthproject.org/azimuth/show/Stratonovich+integral