The Chi-Square Test for Normality allows us to check whether or not a model or theory follows an approximately normal distribution.
The Chi-Square Test for Normality is not as powerful as other more specific tests (like Lilliefors). Still, it is useful and quick way of for checking normality especially when you have a discrete set of data points.
How to Use the Chi-Square Test for Normality.
To apply the Chi-Square Test for Normality to any data set, let your null hypothesis be that your data is sampled from a normal distribution and apply the Chi-Square Goodness of Fit Test. Given your mean and standard deviation, you will need to calculate the expected values under the normal distribution for every data point. Then use the formula
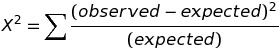
to find the chi-square statistic. Compare this to the critical chi-square value from a chi-square table, given your degrees of freedom and desired alpha level. If your chi-square statistic is larger than the table value, you may conclude your data is not normal.
When not to use the Chi-Square Test for Normality
The Chi Square Test for Normality can only be used if:
- Your expected value for the number of sample observations for each level is greater than 5
- Your data is randomly sampled
- The variable you are studying is categorical.
If your variable is continuous, you will need to bin the data before using the chi-square test for normality.
Alternatives to the Chi-Square Test for Normality
Alternatives to Chi-Square Test for Normality include:
- The Kolmogorov-Smirnov (K-S) test
- The Lilliefors corrected K-S test
- The Shapiro-Wilk test
- The Anderson-Darling test
- The Cramer-von Mises test
- The D’Agostino-Pearson omnibus test
- The Jarque-Bera test
All of these tests have different strength and weaknesses, but the Shapiro Wilk test may have the best power for any given significance.
Sources:
Normality Tests for Statistical Analysis: A Guide for Non-Statisticians
<a href="https://web.archive.org/web/20150630110326/http://instatmy.org.my/downloads/e-jurnal%202/3.pdf" target="_blank"Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. Journal of Statistical Modeling and Analytics
Stattrek Goodness of Fit Test
Stat 452 Statistics: Continuous Methods
Chi-Square Goodness-of-Fit Test in SPSS Statistics