Goodness of Fit > Anderson-Darling Goodness of Fit
What is the Anderson-Darling Test?
The Anderson-Darling Goodness of Fit Test (AD-Test) is a measure of how well your data fits a specified distribution. It’s commonly used as a test for normality.
Performing the AD-Test by Hand
The hypotheses for the AD-test are:
H0: The data comes from a specified distribution.
H1: The data does not come from a specified distribution.
The formula is:
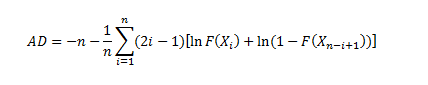
Where:
n = the sample size,
F(x) = CDF for the specified distribution,
i = the ith sample, calculated when the data is sorted in ascending order.
As you can probably see, the test statistic is cumbersome to calculate by hand. The general steps are:
Step 1: Calculate the AD Statistic for each distribution, using the formula above.
Step 2: Find the statistic’s p-value (probability value). The formula for the p-value depends on the value for the AD statistic from Step 1. The following formulas are taken from Agostino and Stephen’s Goodness of Fit Techniques.
| AD statistic | P-Value Formula |
| AD ≥ 0.60 | p = exp(1.2937 – 5.709(AD)+ 0.0186(AD)2 |
| 0.34 < AD* < .60 | p = exp(0.9177 – 4.279(AD) – 1.38(AD)2 |
| 0.20 < AD* < .34 | p = 1 – exp(-8.318 + 42.796(AD)- 59.938(AD)2 |
| AD≤ 0.20 < AD* < .34 | p = 1 – exp(-13.436 + 101.14(AD)- 223.73(AD)2 |
Small p-values (less than your chosen alpha level) means that you can reject the null hypothesis. In other words, the data does not come from the named distribution.
If you are comparing several distributions, choose the one that gives the largest p-value; this is the closest match to your data.
Using Technology
The steps are basically the same, except that software will do the legwork for you and calculate the AD statistic and the p-value. All you have to do is Step 2 above: compare your AD-test p-values to your alpha levels.
- SPSS: The test is not available in SPSS at the time of writing.
- R: use the ‘nortest’ package outlined here.
References
D’Agostino, R. & Stephens, M. (1986). Goodness-of-fit-techniques (Statistics: a Series of Textbooks and Monographs, Vol. 68) 1st Edition. Dekker.