The curly d (∂) is a mathematical symbol that comes from the Cyrillic alphabet. In calculus, it is used in place of the derivative “d” for functions of more than one variable. These multi-variable functions are called partial derivatives.
Curly d for Partial Derivatives
A curly d (∂) is usually used to indicate a partial derivative. It is pronounced as “partial d” when used in this sense.
The formal definition for a partial derivative (Matthews, 2012) is:
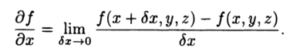
You might also see the following notation for partial derivatives:
∂1 g (x, y)
This is pronounced differently—as “partial d one of g”—but the meaning is exactly the same.
A “partial” derivative (sometimes just called a partial) is taken when you have a function of more than one variable. For example, f(x, y, z) has three variables: x, y, and z. If you take the partial derivative with respect to one variable (say, z), you keep the other two variables constant (x and y). Therefore, you aren’t finding the derivative for all three variables, just a part of them (one third to be exact).
Similarly, you can use a curly d to indicate partial second derivatives: ∂2 f / ∂x2.
Note: A curly d isn’t the only notation used to indicate partials. One alternative is fx(x, y).
Mixed derivatives
The curly d is also used to denote a mixed derivative. Mixed derivatives are like partial derivatives, except that you repeat for all variables. For example, ∂2
References
Körner, T. (2014). Calculus for the Ambitious. Cambridge University Press.
Matthews, P. (2012). Vector Calculus. Springer Science & Business Media.
Stewart, J. & Clegg, D. (2012). Brief Applied Calculus. Cengage Learning.