The Ljung (pronounced Young) Box test (sometimes called the modified Box-Pierce, or just the Box test) is a way to test for the absence of serial autocorrelation, up to a specified lag k.
The test determines whether or not errors are iid (i.e. white noise) or whether there is something more behind them; whether or not the autocorrelations for the errors or residuals are non zero. Essentially, it is a test of lack of fit: if the autocorrelations of the residuals are very small, we say that the model doesn’t show ‘significant lack of fit’.
Ljung Box Test Hypotheses
The null hypothesis of the Box Ljung Test, H0, is that our model does not show lack of fit (or in simple terms—the model is just fine). The alternate hypothesis, Ha, is just that the model does show a lack of fit.
A significant p-value in this test rejects the null hypothesis that the time series isn’t autocorrelated.
Calculating the Ljung Box Test Statistic
Most statistical packages can run a Ljung Box test. For example, in R, you can implement the test with the Box.test function.
To run the Ljung Box test by hand, you must calculate the statistic Q. For a time series Y of length n:
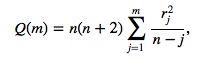
=
Where:
- rj = the accumulated sample autocorrelations,
- m = the time lag.
We reject the null hypothesis and say that the model shows lack of fit if
- χ21-α,h = the value found on the chi-square distribution table for significance level α and h degrees of freedom.
When the Ljung Box test is applied to the residuals of an ARIMA model, the degrees of freedom h must be equal to m-p-q, where p and q are the number of parameters in the ARIMA(p,q) model.
Alternative ways to test for autocorrelation
The Durbin-Watson test is a popular way to test for autocorrelation. However, it can’t be used if you have lagged dependent variables; If you have those, used the Breusch-Pagan-Godfrey test instead.
The Ljung Box test is a modification of the Box Pierce Test. The difference is in how the test statistic is calculated (Kleiber & Zeileis, 2008). Both approximate a chi-squared statistic, based on autocorrelations up to order p.
- Box Pierce test statistic: n * sum of squared autocorrelations,
- Ljung Box test statistic: the squared autocorrelations are weighted at lag j by (n + 2)/(n – j) (j = 1…,p).
References
NIST. Box-Ljung Test. Engineering Statistics Handbook 6.4.4.8.1. Retrieved from https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc4481.htm on July 28, 2014.
Hyndman, Rob J. Thoughts on the Ljung-Box Test. Hyndsight, published online January 24 2014. Retrieved from https://robjhyndman.com/hyndsight/ljung-box-test/ on July 28, 2014.
Kleiber, C. & Zeileis, 2008. Applied Econometrics with R. Springer Science & Business Media, Dec 10, 2008
PennState Statistics. Lesson 3.2: Diagnostics. Stat 510 Applied Time Series Analysis. Retrieved from https://onlinecourses.science.psu.edu/stat510/node/65/ on July 28, 2014.