Contents:
- What is a Linear Function?
- Nonlinear Functions
- Linear Combination
- Linear Relationships / Non Linear
- Linear Equation
- Linear Map
1. What is a Linear Function?
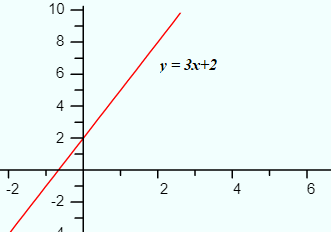
Linear functions are functions that produce a straight line graph.
The equation for a linear function is:
y = mx + b,
Where:
- m = the slope ,
- x = the input variable (the “x” always has an exponent of 1, so these functions are always first degree polynomial.).
- b = where the line intersects the y-axis.
The equation, written in this way, is called the slope-intercept form. These functions can also be written as y = ax + b (common in linear regression) or y = a + bx. These all represent the same graphs.
Examples of linear functions:
- f(x) = x,
- f(x) = 2x – 2,
- f(x) = x + 1.
Domain and Range of a Linear Function
The domain and range of a linear function is usually the set of real numbers. There is an exception: if the function is constant (e.g. f(x) = 2) then the range is restricted to that constant (in this case, 2). Watch this quick video for an explanation and graphical approach:
Limit of a Linear Function
You can find the limit of a linear function in several ways, including:
- Direct substitution,
- Graphing the limit or
- Making a table of values.
A More Formal Approach
You can’t always use a table or calculator in class; Sometimes you have to make a more formal approach, using the definition of a limit. The following example shows how to do this for the function y = 2x + 2. Slightly different steps are needed to solve for infinity, and values other than infinity.
Solving for limits of linear functions approaching values other than infinity.
Example problem: Find the limit of y = 2x + 2 as x tends to 0.
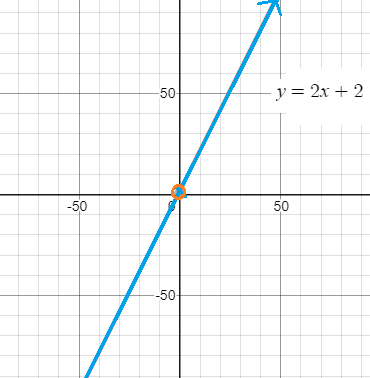
Step 1: Set up an equation for the problem:Use the usual form for a limit, with c equal to 0, and f(x) equal to 2x + 2.
f(x) = 2 x + 2
c = 0
lim f(x) = L = lim 2x + 2
x→c x→0
Step 2: Solve for the limit of the function, using some basic properties of linear functions:
- The limit of ax as x tends to c is equal to ac
- The limit of a as x tends to c is a
- The limit of a + b is equal to the limit of a plus the limit of b
Using this logic, the limit is 2 as x approaches 0.
lim(x→0) 2x + 2 = lim(x→0) 2x + lim(x→0) 2 = 0 + 2 = 2
Solving for limits of linear functions approaching infinity.
Example problem: Find the limit of 2x + 2 as x tends to 0.
Step 1: Repeat the steps as above, but this time solve for the limit as x approaches infinity.
f(x) = 2x + 2
c = ∞
lim(x→&infin) 2x + 2 = lim(x→&infin) 2x + lim(x→&infin) 2 = ∞ = Limit does not exist
Tip: Since the limit goes to infinity when you times infinity by 2, the limit of the function does not exist due to infinity not being a real number. There is one special case where a limit of a linear function can have its limit at infinity taken: y = 0x + b. Since the 0 negates the infinity, the line has a constant limit. This would appear as a horizontal line on the graph.
Back to Top
Nonlinear Functions
What is a Nonlinear Function?
A nonlinear function is defined as one that isn’t a linear function.
Graphically, a linear function is simply any function that produces a straight line graph. More formally, a straight line produced when the dependent variable (y) changes at a constant rate with the independent variable (y), following the equation y = mx + b. In addition, a linear function has a domain and range of all real numbers. A nonlinear function is a function that doesn’t meet these requirements. They are, in a sense, the opposite of linear functions. In other words, a nonlinear function is any function that:
- Has a curved, bent or broken graph,
- Has a domain and range of something other than all real numbers.
- Has a non-constant rate of change,
- Fits any equation other than y = mx + b.
The following functions are all nonlinear:
- Absolute value functions,
- Algebraic Functions,
- Exponential functions,
- Quadratic functions,
- Rational functions.
Most polynomial functions are nonlinear functions with one exception: Algebraically, a linear function is a polynomial with a degree (highest exponent) of 1. They are also known as first degree polynomials. Nonlinear functions are everything else (second degree, third degree, …).
Graph of a NonLinear Function
Linear functions are any functions that produce a straight line graph. So by definition, nonlinear functions produce graphs that aren’t a straight line.
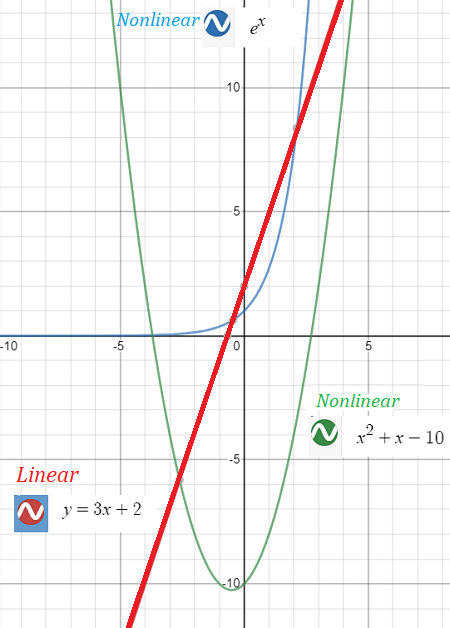
Nonlinear Function vs. Linear Function: Steps
In order to figure out if your function is linear or nonlinear, you have several options. From easiest to hardest, they are:
- Study the equation. If it neatly fits the equation y = mx + b, then it’s linear.
- Graph your function. If there is an obvious straight line (with no dips, curves, or changes in direction), then your function is linear. Otherwise, it’s a nonlinear function.
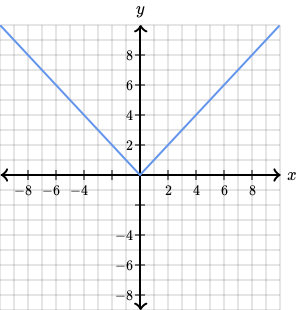
- Calculate the slope of the line between different points (using “rise over run“). You’re looking for the same rate of change between points. Be careful to graph your function after performing this step though, as some functions (like the absolute value function) might appear to have the same rate of change, except that the absolute value function mirrors itself (one side will have a positive slope and the other a negative slope).
Nonlinear Functional Analysis
Nonlinear functional analysis is the study of nonlinear functions. It’s the complement of linear functional analysis. In other words, it’s defined as the study of any function that isn’t linear.
Nonlinear function: References
Desmos Graphing Calculator.
The Biology Project. Linear Functions The Basics. Retrieved January 12, 2021 from: http://www.biology.arizona.edu/biomath/tutorials/linear/Basics_LinearFunctions.html
2. What is a Linear Combination?
In general, a linear combination of a set of terms is where terms are first multiplied by a constant, then added together.
For example, let’s say you have two terms x and y. You might multiply x by 10, and y by 8, to get: 10x + 8y. The expression 10x + 8y is called a linear combination.
The constants placed in front of the terms (10 and 8 in this example) are sometimes called coefficients.
Linear combinations are used frequently because they are easier to conceptualize than some of the more complicated expressions (like those involving division or exponents). Compared to their more complicated relatives, they are also easier to work with mathematically.
Examples of Linear Combinations
Coefficients in a linear combination can be positive, negative or zero. You can also have one term, or more. For example, all of these expressions are valid linear combinations:
- 10x – 8y + 8z
- 10y + 8z
- x + y
- x – z
- 9y
Linear Combination of Vectors
The above definition also extends to vectors. Let’s say that you have two vectors v and w; Each vector is multiplied by a scalar a and b, giving the expression:
av + bw.
The expression av + bw is called a linear combination of v and w.
Using a little linear algebra, you can show linear combinations of more complicated vectors. As an example, the vector (7, 11, 15) is a linear combination of the vectors (1, 1, 1) and (1, 2, 3). The first vector (1, 1, 1) is multiplied by the scalar 3, and the second vector (1, 2, 3) is multiplied by the scalar 4. Adding the results from each multiplied vector, you get:
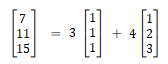
If you’re unfamiliar with matrix multiplication and how the following answer was arrived at, watch the following short video:
Examples of Linear Combinations of Vectors
- 10u – 8v + 8w
- 10u + 8w
- u + v
- u – zw
- 9v
3. Linear Relationships
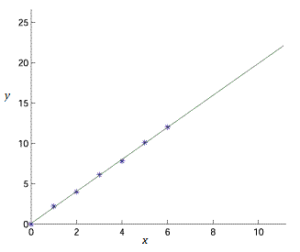
A linear relationship is where you represent the relationship between variables as a line (the word comes from the Latin linearis, from linea “a line”). If you graph linear line, you’ll see a perfectly straight line with no curves.
Non linear relationships are (perhaps not surprisingly) everything else. If there’s no straight line, then it’s non linear.
Linear Equations and Functions
If a set of data has a linear relationship, you can represent it with a linear equation or function.
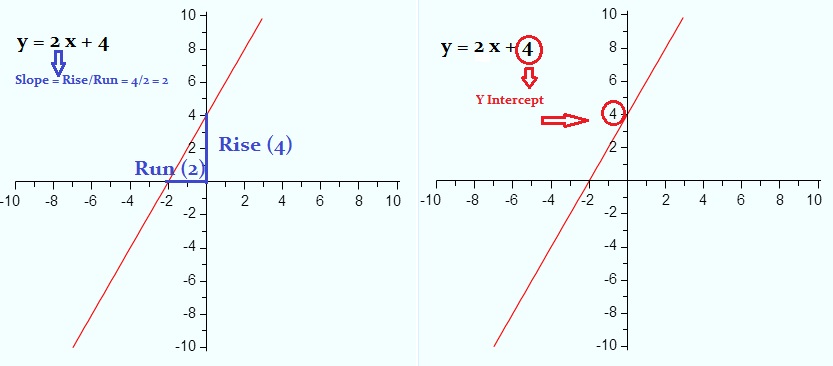
In algebra, you probably came across linear equations and the slope formula. The slope formula looks like this:
y = mx + b
Where:
- “m” = the slope,
- “x” = input (x-value),
- “b” = the y-intercept (where the graphed line crosses the vertical axis).
Linear functions are similar to linear equations. They are functions that can be represented by a straight line graph. A few examples of linear functions that will give a straight line graph:
- f(x) = x,
- f(x) = 2x – 2,
- f(x) = x + 1
The variables in linear functions have linear relationships.
Positive and Negative Linear Relationships
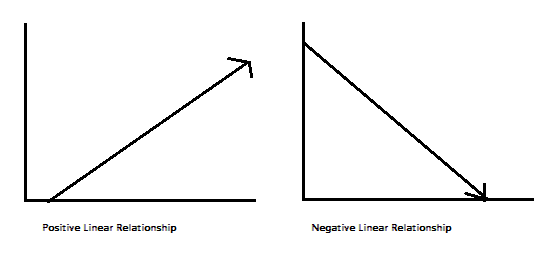
The terms “positive” and “negative” linear relationships refer to the direction the function is traveling.
- Positive linear relationship: The line travels upwards from left to right.
- Negative linear relationship. Travels downwards from left to right.
Finding Linear Relationships from Data
The easiest way to visualize a linear relationship or recognize a linear function with a small set of data is to make a scatter plot.
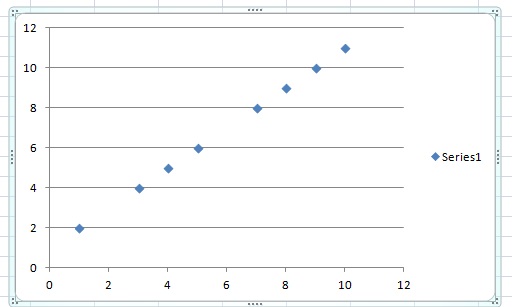
For large sets of data, these are best represented by functions, which you’ll be able to graph on a graphing calculator. You can also plug the numbers into a table on the TI-89 and graph a scatter plot that way.
Collinearity
Definition
A set of points is collinear if you can draw one line through them all. The word literally means “together on a line.” Two points are always collinear: no matter where you draw the two points, you can always draw a straight line between them. A general way to write this is: “Points P1, P2 and P3 are collinear”, which can also be written as “point P1 is collinear with points P2 and P3“.
It goes without saying that points are non-collinear if they do not fall on the same line.
How to Show Points are Collinear
It seems reasonable that if you can draw a line through a set of points, then those points are collinear. The trouble is, those points may not be exactly on the same line. One way to work around this is with the knowledge that the points must satisfy the same linear equation. For example, if you are given the linear equation y = 4x + 16, you know that the points (-4, 0) and (-1, 12) meet the definition because (plugging the x and y values into the equation) we get:
- 0 = 4 * (-4) + 16
- 12 = 4 * (-1) + 16.
An Alternate Method
A second way is to find the slope between the points (i.e. the slopes of the line segments between points P1 and P2, and P2 and P3); if the slopes are the same then the points are collinear. For example, the set of points in the image below fit the definition if the slope of line segment A equals the slope of line segment B.

Example question: Do the points P1 = (−4, 0), P2 = (−1, 12) and P3 = (4, 32) show collinearity?
Step 1: Find the slope for the line segment between the first two points using rise-over-run =(y2 − y1) / (x2 − x1) = (12 − 0)/( −1 − (−4) )= 12 / 3 = 4
Step 2: Find the slope for the line segment between the next two points =(y3 − y2)/(x3 − x2) = (32 − 12)/(4 – (-1))= 20/5 = 4.
Step 3: Compare the slopes you calculated in Steps 1 and 2. The two slopes equal 4, so the points do show collinearity.
Linear Equation

- A constant, or
- The product of a constant and one variable.
They can be written in the form:
a1x1 + … anxn + b = 0
Here:
- x1…, xn are the variables, and there may be any number of them.
- b, a1, … an are the coefficients; they can be constants or expressions, but their expressions can’t include any variable. Some coefficients may be zero, but not all.
Linear Equation Applications
Linear equations are important in physics and engineering. Some physical processes show a direct linear relationship, and even non linear relationships can often be approximated by systems of linear equations. When possible, we like to estimate with them because they are easy to manipulate and calculate with.
Examples of Linear Equations
The simplest linear equation is the one with one variable:
ax + b = 0.
A little bit of algebraic manipulation makes it clear that the unique solution to this linear equation is always -b/a.
If the linear equation has two variables, they are usually called x and y. Then the equation can be written as
ax + by + c = 0
Two independent linear equations will define these two variables completely. Reducing them down to an x = d, y = e form usually requires a small amount of algebraic multiplication. For example, if you are given the two equations
- 3x – y = 7
- 2x + 3y = 1
The first equation can be rearranged as y = 3x – 7.
- Substitute 3x – 7 for y in the second equation, to get:
2x + 3(3x-7) = 1. - Multiply this out to get:
2x + 9x -21 = 1, - Simplify that to get:
11x = 22. - Dividing both sides by 11, we see x is 2.
Finding y is as simple as plugging x = 2 in our first equation, for 6 – y = 7. So y is -1.
Linear equation vs Linear Function
A linear function also has a straight line graph, and can be described by a linear equation. The two terms are so similar that they are often used interchangeably. For all intents and purposes, they are usually the same thing. That said, there is a tiny difference:
- A linear function is a type of function and so must follow certain rules to be classified as a “function”. For example, functions can only have one output for each input.
- On the other hand, equations are just statements that make two things equal, like x = y or 52x = 100. A linear equation also makes two things equal, but produces a straight line. That straight line may, or may not be, a function.
Linear Maps
Contents:
What is a Linear Map?
A linear map is a function from one vector space (the domain) into another (the codomain).
If U is the domain and V is the codomain, we can call our linear transformation T, and define it like this:
T:U → V. If U and V are the same, our linear map is called an endomorphism.
Properties
Every linear function has two special properties. For every u1 and u2 in U
T(u1 + u2) = T(u1) + T(u2).
Also, for all u in U and a in C (i.e., for every constant a)
T(au) = aT(u).
These two properties together, are called linearity. Since linear transformations are operation preserving, we can apply them before or after the addition or scalar multiplication, with no difference in the result.
Examples of a Linear Map
The identity map might be the simplest example of a linear transformation. This is the transformation that maps every point into itself.
The function in the real number space, f(x) = cx, is a linear function. This function can be drawn as a line through the origin.
There are many simple maps that are non linear. For example, for real numbers, the map x: x → x + 1 is non linear. So is the mapping x → x2, also over real numbers.
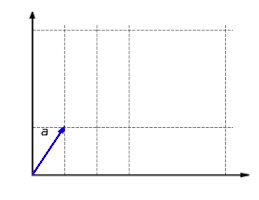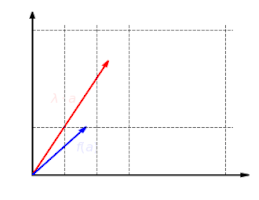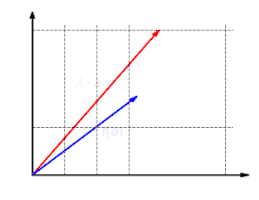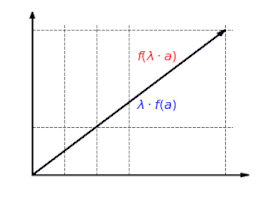
The following series of three images illustrates the linear function f: R2 → R2 with f(x, y) = (2x, y). The y component of the vector remains the same, while the x component is scaled by two, as shown in the first image. The second image shows the additivity of the linear map: it makes no difference whether two vectors are added and then mapped, or whether they are mapped and then added.
The third image demonstrates the linear transformation is homogeneous. Whether the vector is scaled and then mapped, or mapped and then scaled, the final result will be the same.
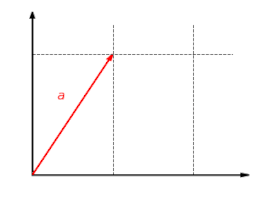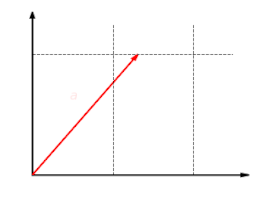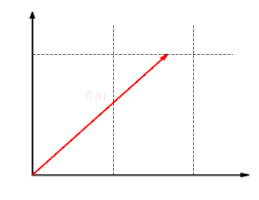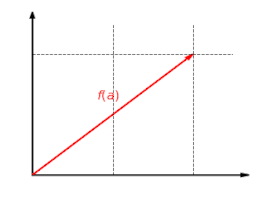
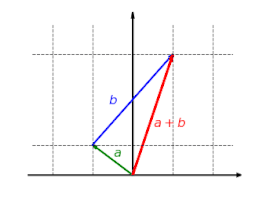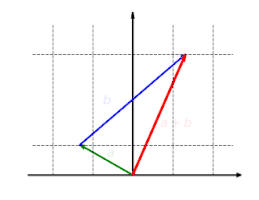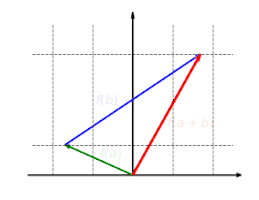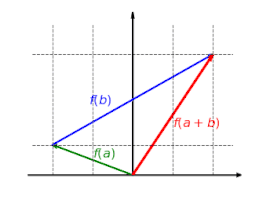
Related article:
Combination of Functions
Linear Function: References
Beezer, Robert A. Linear Transformations. from A First Course in Linear Algebra, version 3.50. Created on December 12, 2015. Retrieved from http://linear.ups.edu/html/section-LT.html on November 9, 2019
Belk, J. Linear Combinations and Span. Retrieved December 1, 2019 from: http://faculty.bard.edu/~belk/math213s14/LinearCombinationsAndSpanRevised.pdf
Larson, R. & Edwards, B. (2009). Calculus. Cengage Learning.
Lian, Bong H. Linear Maps. Retrieved from http://people.brandeis.edu/~lian/TsinghuaMathcamp2014/Chapters8-11.pdf on November 9, 2019
Linear Equations. Chm 621 Curve Fitting. Retrieved from http://www.chem.purdue.edu/courses/chm621/text/curve/matrix/linear/linear.htm on January 5, 2018.
Oldham, K. et al. (2008). An Atlas of Functions: with Equator, the Atlas Function Calculator 2nd Edition. Springer.
Tan, S. Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach. Cengage Learning.
Combinatorics of Fine Geometries.