Calculus Definitions >
Contents (Click to skip to that section):
- Explicit Function
- Implicit Function
- Rewriting an Implicit Function as an Explicit Function
- Explicit Solution
- Implicitization
What is an Explicit Function?
In an explicit function, one variable is defined completely in terms of the other. The general form is:
y = f(x), for a < x < b
Generally, this means that the independent variable is written explicitly in terms of the dependent variable.
Independent variables are the “inputs” for functions. They are usually plotted on the x-axis of a graph. Dependent variables are the “outputs” for functions; They are traditionally plotted on the y-axis.
If your variables are y and x, an explicit function is one where the y can be isolated on the left side of your equation as y = , while the left side of the equation has no other variable except for x.
The following functions are all examples of explicit functions.
- y = 2x + 9,
- y = log x
- y = 2x+ x
What is an Implicit Function?
Functions which are not explicit are called implicit functions; they are functions in which one variable is not defined completely in terms of the other. Some implicit functions can be rewritten as explicit functions. Others cannot.
The function y – x2 = 0 is an implicit function, but it can be rewritten (using basic algebra) as an explicit function as y = x2.
The function y4 +7y 2x−y 2x4 −9x5 = 3 is an implicit function which cannot be written explicitly.
Rewriting an Implicit Function as an Explicit Function
Often in Calculus you’ll be asked to rewrite an implicit function as an explicit function. There is no formula to use on this; you will need to use algebra—adding, subtracting, multiplying, and dividing—to isolate the y (or whatever is your dependent variable) on the left side of the equation.
As you practice this, it will become second nature, and you will easily be able to see what steps to begin with.
For example, suppose you have the implicit equation:
![]()
to turn into explicit form. You will need to first subtract x2 +1 from both sides of the equation, and then take the square root of both sides. The explicit function that results is:
![]()
Remember, though, not every implicit function can be written in explicit terms.
Explicit Solution
When a solution is expressed only in terms of the independent variable and constants, it’s called an explicit solution (it doesn’t necessarily have to be a function!).
As a simple example, the solution y = h ( x )is an explicit solution, because it gives y in terms of x. On the other hand, F(x, y) = 0 is not explicit, because it fails to express y only in terms of x. Another way to put this is that an explicit solution will only have one instance of y on the left hand side of the equation (and only raised to the first power).
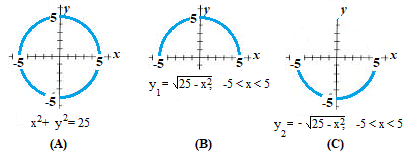
Explicit solutions are preferable for many reasons, including that they are easier to work with. For example, the implicit solution in the image above (the full circle) is not differentiable or integrable, while the half-circles are.
An explicit solution can be algebraic or transcendental. It is algebraic if it only contains powers and roots and transcendental if it contains transcendental functions (e.g. sine function, Bessel function or exponential functions) in addition to powers and roots (Blumel, 2011).
Explicit Solution to ODEs
While explicit solutions can be found in some areas of calculus, it’s rare to find an explicit solution for a system of ordinary differential equations (Shampine et al., 2003). The only possibility for many ODEs is to find an approximate numerical solution (Allaire et al., 2008).
Other Definitions for Explicit Solution
Explicit solutions may be defined slightly differently, depending on what field you are working in. For example, if you’re computing an energy spectrum En of a quantum system in quantum mechanics, an explicit solution has the form:
En = f(n; s), n = 0, 1, …,
Where n is the energy level’s quantum number and s is a set of vectors (Blumel, 2011).
Implicitization
 In mathematics, implicitization means making a variable which was explicit (for example, in a set of parametric equations implicit.
In mathematics, implicitization means making a variable which was explicit (for example, in a set of parametric equations implicit.
If x = x (t) and y = y (t), implicitization would involve solving one of these equations for t, and then substituting that value of t into the other equation. You would end up with just one equation that had no mention of t. The idea is very similar to solving simultaneous equations in algebra, so if you can solve those, you can perform implicitization.
Examples of Implicitization
Suppose you wanted to implicitize x = a + b t and y = t2.
Step 1: Solve the first equation for t.
- Subtract -a from both sides to get (x – a) = bt.
- Divide by b, to get t= (x – a)/ b.
Step 2: Insert this into your second equation. y = t2, to end up with y = (x – a)2 / b2.
This is the implicit equation; notice it doesn’t include the variable t.
For another example, let’s say you wanted to implicitize the set of equations y = a sin (t), x = a cos(t). Remember that cos(t)2 + sin(t)2 = (the Pythagorean trigonometric identity.) Since cos(t) = x / a and sin(t) = y / a, we rewrite the Pythagorean identity as (x / a)2 + (y / a)2 = 1.
Not all implicitization problems are solvable. One example of a problem which can’t be implicitized into a single equation is the set of parametric equations x = α cos θ eβθ y = α sin θ eβθ. It’s a 2-parameter family of logarithmic spiral curves, but there is no one polynomial equation that describes it.
Higher Dimension Implicitization
Higher dimension implicitization involves analyzing more than one parameter or more than two coordinates. In these cases you can use a Gröbner basis computation to implicitize. A Gröbner basis computation is essentially a generalization of Euclidean algebra as it relates to polynomials.
References
Allaire, G. et al. Numerical Linear Algebra. Springer, New York. 2008.
Blumel, R. Advanced Quantum Mechanics The Classical-Quantum Connection. Jones & Bartlett Learning. 2011.
Shampine et al., (2003). Solving ODEs with MATLAB. Cambridge University Press.
Explicit and Implicit Functions. Retrieved from
https://www.nr.edu/chalmeta/271DE/Section%204.5.pdf on December 9, 2019.
Basak Tathagata. Explicit Function. Teaching Math Notes. Retrieved from https://orion.math.iastate.edu/tathagat/teaching/18_math165/165notes-week7.pdf on
Very useful. Thank you for the information and your efforts.
it was so helpful for my college seminar