Thinking of using the TI 89 for statistics? The TI 89 is a hand held calculator that can be used for just about any math class, from algebra to complex analysis. If you’re a math major, you probably own one. But even if you aren’t a math major, it can be useful to help you calculate many stats problems easily.

There are two types of TI 89:
The TI 89 Titanium is packed with helpful and useful features. It boasts support for nearly every major high-school and college class. This model has a large screen with icons rather than menus. That means it’s easy to find what you are looking for. The regular TI 89 is almost identical. However, the Titanium has increased memory size, speed, and a direct USB connection.
Looking for a specific topic? Hit CRTL + F on your keyboard, then type in a search term in the search box.
TI 89 for Statistics: Basics
- How to Simplify on the TI 89 (CalculusHowTo.com)
- How to Expand a Binomial on the TI 89
- Error Codes (CalculusHowTo.com)
TI 89 for Statistics: Probability
- How to Calculate Binomial Probability on the TI-89 Graphing Calculator
- How to Use the TI-89 to calculate combinations
TI 89 for Statistics: Descriptive Statistics
- How to Find a Five Number Summary and Create a BoxPlot on the TI-89 Graphing Calculator
- How to Calculate Mean and Standard Deviation for a Binomial Distribution on the TI-89
- How to Graph a Cumulative Frequency Table on the TI-89 Calculator
- How to Create a Frequency Chart or Histogram on the TI-89 Titanium
- How to Find Q1, Q3 and the Interquartile Range on the TI-89 calculator
- How to Make a Scatter Plot on the TI-89 Calculator
- How to Find the Mean, Median, and Mode on the TI-89 Calculator
- Variance on a TI-89 Calculator
- Standard Deviation on the TI-89 Calculator
TI 89 for Statistics: Tests, Regression
- Regression on the TI-89
- Z Score on the TI 89 (Left Tailed Test)
- How to Find a T-Distribution on the TI 89
- How to Find an F Distribution on the TI89
- How to Find a Confidence Interval for a Mean (Known Standard Deviation)
- Normal Distribution Word Problems on the TI-89: Finding Cut Off Points For a Top Percentage
- How to Use a TI-89 Graphing Calculator for a Hypothesis Test on a Mean
- How to Use a TI-89 Calculator For Large Sample Hypothesis Testing (Proportion)
- How to Use a TI-89 for Figuring out Confidence Intervals
- Solving Central Limit Theorem Word Problems on the TI-89 Graphing Calculator
- How to Find a Critical Value on a Ti-89 Titanium (Left-Tailed test)
Calculus
- Finding asymptotes.
- How to find derivatives.
- How to Graph and evaluate a Function
- Intersection and Trace on the TI-89
- Create a Table of Function Values on the TI-89
- Find Limits on the TI 89
- Piecewise Functions TI 89 “when(” Command
- How to Find Roots/Zeros of a Function on the TI-89
- Error Codes
- How To Simplify An Expression
Algebra
TI 89 for Statistics: How To Factor The Difference Of Two Squares On The TI-89
Factoring the difference of two squares probably brings back nightmares from elementary algebra. By hand, it involves identifying common factors and often a long (nasty-looking) calculation that’s prone to errors. Technically, a term is a perfect square when the number in front of the variables (the numerical coefficient) is a perfect square and the exponents are even numbers. If you want to factor the difference of two squares, it can be done easily on the TI-89 graphing calculator and is as simple as pressing a few buttons.
Example Problem: Factor the following function: f(x) = y2 – 16
Step 1: Press the HOME key.
Step 2: Press F2 and then 2 to access the “factor” function.
Step 3:
(Y^2)-(16))
Step 4: Press ENTER. Your answer will be (y – 4) (y + 4).
That’s it! You’re done!
The TI graphing calculators are recommended for AP statistics (and are allowed to be taken into exams). You can get one on eBay or Amazon.com for about $90 (don’t buy it from a college bookstore—you’ll pay full price, $150+!).
Why should you buy a TI-89 Calculator for your elementary statistics course?
Here is an example of how easy the TI-89 makes statistics:
Variance and Standard Deviation problems are perhaps the most basic problems elementary statistics students are taught. They are taught in the first couple days of any statistics course. Here’s the difference between calculating variance and standard deviation manually, versus using the TI-89:
Find the variance and standard deviation of 12, 48, 79, 99, 101.
Manually
Step 1: Add the numbers in the list.
12 + 48 + 79 + 99 + 101 = 339
Step 2: Square the sum, and divide by the number of items in the data set:
339 × 339 = 114,921
114,921 / 5 = 22,984.2
Step 3: Take your original numbers from step 1, square them individually, and add them up:
(12 × 12) + (48 × 48) + (79 × 79) + (99 × 99) + (101 × 101) = 28,691
Are you getting bored yet?
Step 4: Subtract the amount in step 2 from the amount in step 3:
28,691 – 22,984.2 = 5,706.799999999999
Step 5: Subtract 1 from the number of items in my data set:
5 – 1 = 4
Step 6: Divide by the number in step 4 by the number in step 5:
5,706.799999999999 / 4 = 1,426.6999999999998
That’s the Variance.
Step 7: Take the square root of the number from step 6.
√(1,426.6999999999998) = 37.77168251481525
That’s the Standard Deviation.
Using the TI-89
Step 1: Enter the list of numbers.
Step 2: Select the Variance or Standard Deviation functions, depending on which you want.
Step 3: Yawn and stretch. There is no step 3! You’re done!
Still not convinced that the TI-89 will save you time and stress?
Let’s look at how the calculator can help you with a more complex problem, like Linear Regression. The calculation for Linear Regression will take you 15 to 30 minutes depending on how confident you are with your math skills. You can find a linear equation on a TI-89 in less than a minute!
Here are the methods, side by side:
Manual Linear Regression
Step 1: Make a chart of your data, filling in the columns in the same way as you would fill in the chart if you were finding the Pearson’s Correlation Coefficient.
| Subject | Age x | Glucose Level y | xy | x2 | y2 |
|---|---|---|---|---|---|
| 1 | 43 | 99 | 4257 | 1849 | 9801 |
| 2 | 21 | 65 | 1365 | 441 | 4225 |
| 3 | 25 | 79 | 1975 | 625 | 6241 |
| 4 | 42 | 75 | 3150 | 1764 | 5625 |
| 5 | 57 | 87 | 4959 | 3249 | 7569 |
| 6 | 59 | 81 | 4779 | 3481 | 6561 |
| Σ | 247 | 486 | 20485 | 11409 | 40022 |
From the above table, Σx = 247, Σy = 486, Σxy = 20485, Σx2 = 11409, Σy2 = 40022. n is the sample size (6, in our case).
Step 2. Use the following equations to find a and b.
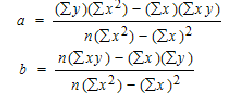
Find a:
- ((486 × 11,409) – ((247 × 20,485)) / 6 (11,409) – 2472)
- 5,544,774 – (5,059,795 / 7,445)
- =553,794
Find b:
- (6(20,485) – (247 × 486)) / (6 (11409) – 2472)
- (122,910 – 120,042) / 68,454 – 2472
- 2,868 / 7,445
- = .385225
Step 3: Insert the values into the equation.
y’ = a + bx
y’ = 553,794 + .385225x
TI-89 Linear Regression
Step 1: Enter the X and Y values into the TI-89.
Step 2: Select the Linear Regression Function from the menu.
Expecting more? Sorry to disappoint: you’re done.
Think about how much exam time the TI-89 will save you!
I have built online calculators for a couple of common statistics calculations, but no online calculator can compare with the hundreds of functions available in the TI-89. Plus, you aren’t typically allowed to use online resources during an exam (and even if you are, what happens if the internet goes down?).
Lost your guidebook? Check out the TI-site. You can download a new guidebook here.
Check out our Youtube channel for more stats tips and TI 89 for statistics topics.