Statistics Definitions > Yates Correction
The Yates correction is made to account for the fact that both Pearson’s chi-square test and McNemar’s test are biased upwards for a 2 x 2 contingency table. An upwards bias tends to make results larger than they should be. If you are creating a 2 x 2 contingency table that uses either of these two tests, the Yates correction is usually recommended, especially if the expected cell frequencies are below 10 (some authors put that figure at 5).
Watch the video for an example.
Why is the Yates correction used?
Chi2 tests are biased upwards when used on 2 x 2 contingency tables. The reason is that the statistical Chi2 distribution is continuous and the 2 x 2 contingency table is dichotomous (in other words, it isn’t continuous, there are two variables). The math proving this is beyond the scope of this site (we’d be delving into some serious proofs here); All you really need to know is that if your expected cell frequencies are below 10, you probably should be using the Yates correction.
Calculating the Yates Correction
In order to apply the Yates correction, subtract .5 from the numerical difference between the observed frequencies and expected frequencies. The formula looks complicated, but it’s just the Chi2 formula with the .5 subtraction:
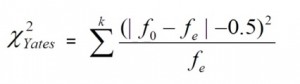
You must do this for all four cells of your calculation.
Example: Your contingency table gives you observed and expected cell frequency values of:
- Cell 1: 220, 210.22
- Cell 2: 7, 9.12
- Cell 3: 2, .22
- Cell 4: 21, 17.12
The Yates correction would be:
- Cell 1: (|220 – 210.22|-.5)2/210.22
- Cell 2: (|7 – 9.12|-.5)2/9.12
- Cell 3: (|2 – .22|-.5)2/.22
- Cell 4: (|21 – 17.12|-.5)2/17.12
- = 0.41 + 0.29 + 7.44 + 0.67
- = 8.81
Arguments for why the Yates Correction should not be used
Although some people recommend that you should use the correction only if your expected cell frequency is below 10 or even 5, others recommend that you don’t use it at all. A large body of research has found that the correction is too strict. Several researchers, including Yates, have used known statistical data to test whether the correction works. If you are using a statistical program like R to calculate the critical chi-square value for a contingency table, the program will usually force you to incorporate the correction. However, knowing that the correction may be too strict allows you to make a judgment call on your data.
If you choose not to use the correction, you may want to cite one of the following papers, which argue that the Yates Correction is too strict:
Camilli, G. & Hopkins, K. D. (1979). Testing for association in 2 * 2 contingency tables with very small sample sizes. Psychological Bulletin, 86, 1011-1014. Online article.
Larntz, K. (1978). Small sample comparisons of exact levels for chi-square goodness of fit statistics. Journal of the American Statistical Association, 73, 253-263. Online article.
Thompson, B. (1988). Misuse of chi-square contingency-table test statistics. Educational and Psychological Research, 8(1), 39-49. Online article.
This article gives a summary of the arguments:
Hitchcock, David B. (2009). Yates and Contingency Tables: 75 Years Later. Retrieved 4/8/2015 from: University of South Carolina.
References
Greenwood, P. (1996). A Guide to Chi-Squared Testing (Wiley Series in Probability and Statistics) 1st Edition. Wiley Interscience.
Yates, F. (1934). Contingency tables. Journal of the Royal Statistical Society, 1, 217-235.